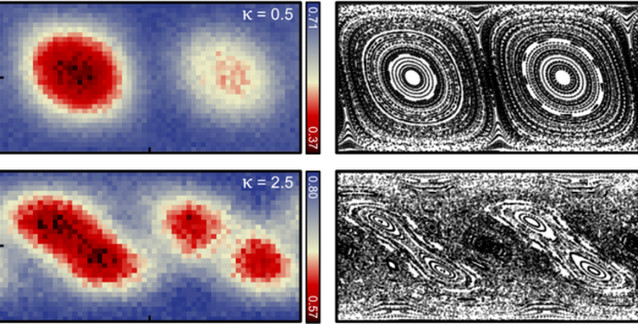
Kaos kelimesi hepimiz için farklı anlamlar ifade eder. Hafta içi iş çıkış saatlerinde Mecidiyeköy ya da çocuklarla dolu bir sınıf bize kaosu çağrıştırabilir.

Kaotik bir dünyada, ne bekleyeceğimizi asla bilemeyiz. Rastgele etkiler, rastgele olaylara sebebiyet verir. Ancak, fizik ve iklim bilimi ile bağlantılı olarak kaos, daha derin bir anlam barındırır ve hava durumu gibi belirli sistemlerin temelde nasıl tahmin edilemez olduğuyla doğrudan ilgilidir.

Kaos Teorisi, “doğal olarak öngörülemeyen” sistemlerin davranışını tahmin etme bilimi olarak tanımlanır ve tanımı gereği bile içinde derin bir çelişki barındırır. Bir kaos denizinden; örneğin, insan kalbinin atışı ve asteroitlerin yörüngeleri gibi çeşitli doğal sistemlerin karmaşık işleyişine açılan bir pencereden, güzelce düzenlenmiş yapıları çıkarmamızı sağlayan matematiksel bir araç takımıdır.

Modern matematiğin en muhteşem alanlarından birine hoş geldiniz.

Kaos Teorisi’nin merkezinde, düzen ve kaosun her zaman taban tabana zıt olmadığına dair büyüleyici bir fikir vardır. Kaotik sistemler, ikisinin yakın bir karışımıdır: dışarıdan, öngörülemeyen ve kaotik davranışlar sergilerler, ancak iç işleyişi ortaya çıkarırlar ve saat gibi işleyen mükemmel deterministik bir denklem seti keşfedersiniz. Bazı sistemler, çalkantılı ve kaotik nedenlerden ortaya çıkan düzenli etkilerle bu önermeyi tersine çevirir.

Peki, küçük ölçekteki düzen, nasıl olur da daha büyük ölçekte kaos yaratabilir? Ve “rastgelelik” ile kaos içinde gizlenmiş düzenli paternler arasındaki farkı nasıl anlayabiliriz? Cevaplar, çoğu kaotik sistem tarafından paylaşılan ortak özelliklerde bulunabilir.

Kelebek Etkisi

1961'deEdward Lorenz adındaki bir meteorolog muhteşem bir keşif yaptı. Lorenz, hava durumunu daha doğru bir şekilde tahmin etmek için bilgisayarların yeni yeni keşfedilen gücünü kullanıyordu. Mevcut hava durumunu temsil eden bir dizi sayı ile hava durumunu birkaç dakika önceden tahmin edebilen bir matematiksel model yarattı. Bu bilgisayar programı çalışır duruma geldiğinde, Lorenz, tahmin edilen hava durumunu bilgisayara tekrar tekrar yükleyerek uzun vadeli tahminler üretebildi ve programı her çalıştırmada daha da uzak geleceğe yönelik tahminlerde bulundu. Tahminler, dakikalara, günlere ve ardından haftalara eklendi.

Bir gün, Lorenz modellerinden birini yeniden çalıştırmaya karar verdi. Bu modelinde, zaman kazanmak adına sıfırdan başlamamaya karar veren meteorolog, bunun yerine, bilgisayarın tahmin sonuçlarının ilk yarısını başlangıç noktası olarak kullandı. Hak edilmiş bir kahve molasından sonra yerine döndüğünde beklenmedik bir şey keşfetti. Bilgisayarın yeni tahminleri eskisi gibi başlasa da, iki tahmin grubu kısa sürede büyük ölçüde farklılaşmaya başladı. Yanlış giden şey neydi?

Lorenz kısa süre sonra, bilgisayarın sayıları altı ondalık basamak kullanarak hesapladığını, fakat tahminleri üç ondalık basamağa yazdırdığını fark etti. Böylece, ikinci tura 0,506 sayısıyla başlarken, orijinalde 0,506127 sayısını kullanmıştı. Binde bir olan bu fark, bir kelebeğin kanat çırpışının yüzünüzdeki esintinin etkisine benzer.

Başlangıçta hava koşulları hemen hemen aynı gözüküyordu. Fakat Lorenz kaosun tohumlarını çoktan keşfetmişti. Sorunsuz sistemlerde (kaotik etkiler olmadan) küçük farklılıklar sadece küçük etkilere sebep olurken; Lorenz'in denklemleri, hataların zamanla istikrarlı bir şekilde büyümesine neden oluyordu. Bu da, mevcut hava durumu hesaplamalarındaki küçük hataların küçük olarak kalmayacağı; tahminleri tamamen boşa çıkarana kadar bilgisayara her veri beslemesinde boyutlarının acımasızca artacağı anlamına geliyordu. Lorenz bu etkiyi, kanatlarını çırpan ve dünyanın öbür ucunda bir kasırganın oluşmasına neden olan bir kelebeğe benzetmiştir.

“Kelebek etkisini" kendiniz görmek isterseniz, bunun güzel bir yolu bilardo oynamaktır. İlk atışta ne kadar tutarlı olursanız olun, beyaz topa vurduğunuz hız ve açıdaki en küçük değişiklik, diğer bilardo toplarının her seferinde çılgınca farklı yönlere dağılmasına neden olacaktır. Yani bu sistemlerde en küçük farklılıklar, kaotik bir sistemin ayırt edici özelliği olan büyük etkiler üretir. Bu noktada, bilardo toplarının nasıl hareket ettiğini belirleyen fizik yasalarının kesin ve net olduğunu belirtmekte de fayda var: rastgeleliğe yer bırakmazlar. İlk bakışta rastgele gibi görünen bir şey tamamen determinist tir; bize rastgele görünür çünkü fark edilmeyen tüm değişiklikler birleşip farkı oluşturur. Bu küçük farklılıkların birleşme hızı, her kaotik sistemde, artık davranışını doğru bir şekilde tahmin edemeyeceğimiz bir süre boyunca bir tahmin ufku sağlar. Günümüzde hava durumlarında sürekli gelişen ölçüm cihazları ve modelleri sayesinde tahmin ufku yaklaşık 1 haftadır. 50 yıl kadar önce ise 18 saatti. Bilgisayarlar ve yazılımlar ne kadar iyi olursa olsun, ulaşabileceğimiz sınırın ise 2 hafta olduğuna inanılıyor.

Şaşırtıcı bir şekilde, güneş sistemi de, Kaos Teorisi ortaya çıkmadan çok önce keşfedilen, yüz milyon yıllık bir tahmin ufku olan kaotik bir sistemdir. Newton'un yerçekimi teorisi, karşılıklı çekim altında iki gezegensel cismin nasıl yörüngede kalacağını mükemmel bir şekilde tahmin ederken; 1887'de Fransız matematikçi Henri Poincaré, bu karışıma üçüncü bir cisim eklemenin denklemleri çözülemez hâle getirdiğini gösterdi. Gezegenlerin bu dansının uzun bir tahmin ufku olmasına rağmen kaosun etkileri göz ardı edilemez, çünkü gezegenler arasındaki yerçekimlerinin karmaşık etkileşimi, asteroitlerin yörüngeleri üzerinde de büyük bir etkiye sahiptir. Asteroitlere göz kulak olmak zor olsa da harcanan tüm çabalara değer, çünkü bu tür kaotik etmenler, bir gün istenmeyen bir sürprizi aniden yolumuza çıkarabilir.

Yıllar boyunca, bize kaos yaratmanın aslında ne kadar kolay olduğunu gösteren bir dizi keşif yapıldı. Bunlardan biri de double pendulum yani çift sarkaç sistemiydi. Normalde eski bir saatin sallanan sarkacından daha öngörülebilir bir şey olamaz çünkü başlangıç ​​koşullarındaki küçük değişiklikler sistemin uzun vadeli sonucuna çok fazla etki etmeyecektir. Ancak bir sarkacı, yarısına başka bir aks ekleyerek ayırırsanız salınım çılgın bir hâl alır ve tahmin edilemez hâle gelir.

Isaac Newton, fiziği, "bir kez harekete geçtiğinde önceden belirlenmiş bir sonuca yol açacak, saat gibi işleyen bir evren kurallarını yöneten bir kurallar dizisi" olarak tasavvur etmişti. Ancak kaos teorisi, en katı kuralların ve neredeyse mükemmel bilgilerin bile öngörülemeyen sonuçlara yol açabileceğini kanıtlıyor.