Doğa Gerçekten Kaotik ve Fraktal mıdır?
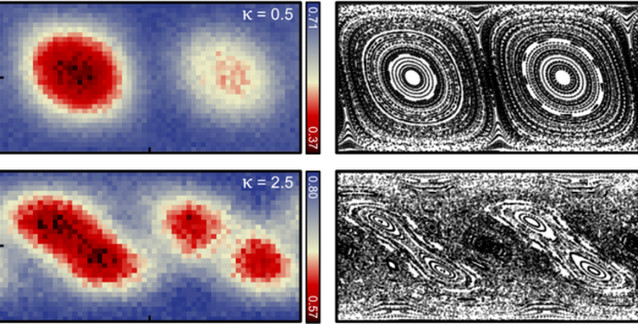
Yaygın kullanımda, "kaos" kelimesi düzensizlik anlamına gelir. Peki bu fizik açısından da böyle mi? Aslında değil. Fizikteki kaos kavramı "öngörülemez" anlamına gelir ve durumu zamanla değişen fiziksel sistemler için kullanılır.
Bir fiziksel sistem basitçe, kendisini çevreleyen ortamdan bir şekilde yalıtılmış olarak düşünmeyi tercih ettiğimiz, evrenin bir dilimi olarak düşünülebilir. Kimi zaman sistemi çevreleyen ortamın toplam etkisini kabul ederiz ama daha sıklıkla sistemin yalıtılmış olduğunu kabul etmeyi seçeriz. Peki gerçek yalıtım mümkün müdür? Cevap hayır; gerçek yalıtım yapaydır.
Örneğin; bir kristal, geleneksel olarak üç uzamsal boyutta sınırsızca periyodik olarak düzenli bir yapıya sahip bir katı olarak tanımlanır. Böyle "mükemmel derecede düzenli" bir sistemin var olabildiğini (aslında olamaz) kabul etsek bile böyle bir sistem gerçekte sonlu boyuta sahip olacaktır. Bu sayede bu mükemmel yapıların gerçekten çok hayali olduğunu fark etmek kolay olur: Doğada bulunduğu haliyle kristaller sadece sonlu boyutta olmakla kalmazlar, ayrıca pek çok kusurlar içerir ve mükemmelden kat kat uzaktırlar. Şansa bakın ki, mükemmellik öznel bir kavramdır ve fizikte bir kristal, atom merkezlerini temsil eden bir dizi nokta üzerinde tekrarlanabilen simetri operasyonlarını tanımlayan denklemler şeklinde gösterilen, bir kurallar dizisi tarafından tanımlanır. Bunlar bir sonsuz, üç boyutlu, periyodik yapıyı açıklarlar.
Bu kurallar keyfi olarak "mükemmel" şeklinde tanımlanır çünkü sınırsızca kendi kendini tekrarlayabilen örüntüleri açıklarlar. Bu sayede herhangi bir gerçek yapı, kıyaslama yapıldığında oldukça kusurlu kalır. Eğer modelimiz kusurlara izin vermiyorsa, gerçek bir yapıdaki süreksizlikleri ve düzensizlikleri nasıl öngörebiliriz? Öngöremeyiz. Böylece tanımladığımız sistem “kaotik” olarak etiketlenir, çünkü bahsi geçen "mükemmel" kurallar ile öngörülemezler. Böylelikle kaos sorununun gerçeklikle bir alakası olmadığı, daha çok insan yorumuyla alakalı olduğu sonucuna varabiliriz.
Böyle "mükemmel dışılıklar" ilginç bir olguya daha yol açabilir: Doğanın fraktal geometrisi; ki bu ayrıca her yerde bulunan bu yapıları çalışan ünlü bir matematikçinin yazdığı kitabın adıdır: Benoit Mandelbrot.
Fraktal nedir? Fraktaller teknik olarak kesirli boyutlara sahip geometrik yapılardır. Örneğin; 2,3. Bunu anlayabilmek için bir örnek vermek yerinde olur: Bir doğruyu takip etmenizin söylendiğini varsayın. İlkokuldan biliyoruz ki bir doğru tek boyutta sonsuz adet noktadan ibarettir ve böylece, bir doğrunun kendisi de sonsuz olur.
Gerçekten düz bir çizgi çizebilir misiniz? Hayır. Fakat muhtemelen bir doğru parçasını çizebilirsiniz. Bir doğru parçası, iki uç nokta ile sınırlanmış sonsuz noktalar dizisidir. Eğer bir doğru için tüm bir boyutu takip etmeniz gerekirken, bir doğru parçası için bundan daha da azına ihtiyacınız vardır.
Diğer bir deyişle, doğru parçasını takip etmek 0 ile 1 arasında bir kesirde boyuta ihtiyacınız vardır. Böylelikle bir doğru parçası oldukça basit ama yine de fraktal bir geometri oluşturur. Doğru denklemini kullanarak (y = a * x + b) tek bir boyutta yer alan bütün olası doğru parçalarını öngörebilir misiniz? Evet. Fakat böylesi bir denklem, doğru parçasının uç noktalarının koordinatları için sonsuz, sayılamaz, hesaplanamaz ve doğal olarak düzenlenemez bir değerler dizisi oluşturur.
O halde doğanın fraktal olarak göründüğünü güvenle söyleyebiliriz. Fakat gerçekten de öyle midir? Bu sorunun cevabının fizikten çok felsefeyle ilgisi olduğu ve doğruluğu tartışılabilir. Peki ya fraktaller, sonsuzluğu kavramaya yönelik doğuştan gelen yetersizliğimize yönelik yeni gelişen bir özellikse?- Is nature really chaotic and fractal, or did we just imagine it? https://cosmosmagazine.com/physics/is-nature-really-chaotic-and-fractal-or-did-we-just-imagine-it
Dilediğiniz miktarda aylık veya tek seferlik bağış yapabilirsiniz.
Destek OlBunlar da İlginizi Çekebilir