Sinirbilim
21 Haziran 2017
Beyin Ağlarındaki Çok Boyutlu Matematiksel Evren
Sinirbilimde daha önce kullanılmamış cebirsel topolojiyi kullanarak, Mavi Beyin Projesi’nden bir ekip, beyin ağları içerisindeki çok boyutlu geometrik yapılar ve boşlukların evr...
Mavi Beyin projesi ekibi, insan beyninin karmaşıklığını açıklayabilecek ilginç bir fikir ileri sürdü. Karmaşık bağlantıları grafiklere döken matematiksel bir dal olan cebirsel topoloji kullanan araştırmacılar, nöral ağların yapısından karmaşık fonksiyonlar elde edebilecekleri bir yol buldu. Araştırmacılar, fiziksel olarak 3 boyutlu uzayda bulunan beynin içsel bağlantılarının matematiksel karmaşıklığını ifade edecek topolojik uzayın bazen 7 ya da 11 boyutlu olması gerektiğini belirtiyorlar. Yani nöral bağlantıların karmaşıklığı sanılanan çok ötesinde ama yine de onları tanımlayacak bir dile sahip olabiliriz.
Topolojik dilde "boyut" sözcüğü karmaşıklığı tanımlamak için kullanılıyor. Singularity Hub’a konuşan, EPFL’den linsanüstü öğrencisi Max Nolte, “Çalışmamızda boyut sözcüğü, uzay boyutlarını tanımlamıyor; açıklamak istediğimiz geometrik nesnelerin topolojik boyutunu tanımlıyor. 7 veya 11 boyutlu simpleksler halen üç boyutlu fiziksel uzayda yerleşik olarak bulunuyor,” diyor. Yani burada boyut sözcüğü, simplekslerin karmaşıklığını anlatıyor.
Frontiers in Computational Neuroscience dergisinde yayımlanan makale, yapıların bir grup nöronun bir takım oluşturmasıyla açığa çıktığını gösteriyor. Her bir nöron, her bir diğer nörona, kesin bir geometrik nesne oluşturan spesifik bir şekilde bağlanıyor. Takımda ne kadar fazla nöron varsa, geometrik nesne o kadar fazla boyuta (karmaşıklığa) sahip oluyor. Beynin küçük bir parçasında 7 boyuta varan boyutlarda on milyonlarca böyle nesneler bulunuyor. Hatta bazı ağlarda, 11 boyutlu nesneler bile bulunabiliyor.
Bu keşif, beynin anlaşılmasının neden bu kadar zor olduğunu açıklayabilir. Sinirsel ağları çalışmak için uygulanan matematik, genellikle bu tür yüksek boyutlu geometrik nesneleri ve boşlukları tespit edemiyordu.
Eğer 4 boyutlu dünyalar bile zihnimizi bulandırıyorsa; 5, 6 ve daha yüksek boyutların pek çoğumuz için kavranması fazlasıyla karmaşıktır. İşte burada cebirsel topoloji devreye giriyor. Cebirsel topoloji, herhangi bir sayıdaki boyutları açıklamak için kullanılan matematik dalıdır. Cebirsel topolojiyi, beyin ağlarını çalışmak için kullanan matematikçileri, EPFL’den Kathryn Hess ve Aberdeen Üniversitesi’nden Ran Levi.
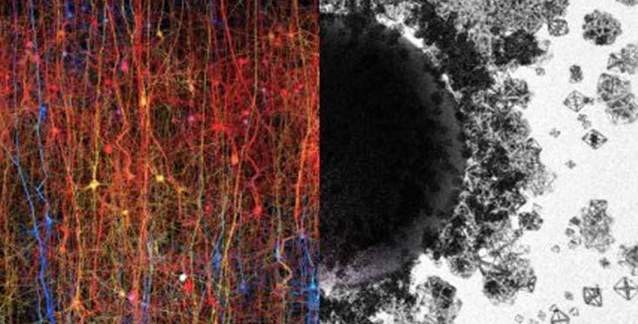
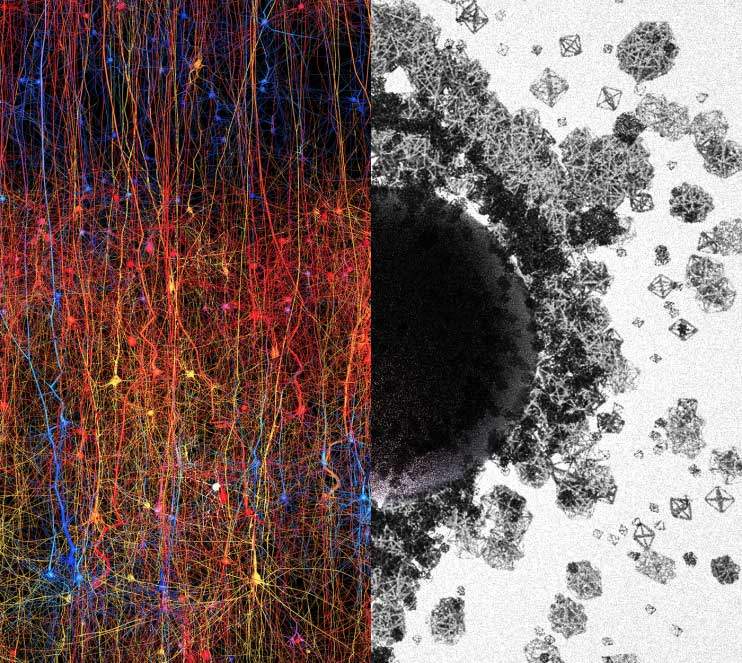 Görsel, görüntülemeyecek bir şeyi göstermeye çalışıyor, çok boyutlu yapıların ve boşlukların evrenini. Sol tarafta, beynin en fazla evrimleşmiş parçası neokorteksin dijital bir kopyası yer alıyor. Sağ tarafta ise 1’den 7’ye kadar, hatta daha da fazla boyutlarda yapıları temsil etmeye çalışan değişik boyutlarda ve geometrilerde şekiller yer alıyor. Ortada yer alan “kara delik” çok boyutlu boşluklar yani oyuklar kompleksini sembolize etmek için kullanıldı. Mavi Beyin Projesi’ndeki araştırmacılar son makalelerinde, bu tür oyuklara bağlanan nöron gruplarının, sinirsel yapılar ve işlevler arasındaki kayıp bağlantıyı sağladığını rapor ediyorlar.
Görsel, görüntülemeyecek bir şeyi göstermeye çalışıyor, çok boyutlu yapıların ve boşlukların evrenini. Sol tarafta, beynin en fazla evrimleşmiş parçası neokorteksin dijital bir kopyası yer alıyor. Sağ tarafta ise 1’den 7’ye kadar, hatta daha da fazla boyutlarda yapıları temsil etmeye çalışan değişik boyutlarda ve geometrilerde şekiller yer alıyor. Ortada yer alan “kara delik” çok boyutlu boşluklar yani oyuklar kompleksini sembolize etmek için kullanıldı. Mavi Beyin Projesi’ndeki araştırmacılar son makalelerinde, bu tür oyuklara bağlanan nöron gruplarının, sinirsel yapılar ve işlevler arasındaki kayıp bağlantıyı sağladığını rapor ediyorlar.
Görsel Telif: Topology concept - Courtesy of Blue Brain Project Görsel, görüntülemeyecek bir şeyi göstermeye çalışıyor, çok boyutlu yapıların ve boşlukların evrenini. Sol tarafta, beynin en fazla evrimleşmiş parçası neokorteksin dijital bir kopyası yer alıyor. Sağ tarafta ise 1’den 7’ye kadar, hatta daha da fazla boyutlarda yapıları temsil etmeye çalışan değişik boyutlarda ve geometrilerde şekiller yer alıyor. Ortada yer alan “kara delik” çok boyutlu boşluklar yani oyuklar kompleksini sembolize etmek için kullanıldı. Mavi Beyin Projesi’ndeki araştırmacılar son makalelerinde, bu tür oyuklara bağlanan nöron gruplarının, sinirsel yapılar ve işlevler arasındaki kayıp bağlantıyı sağladığını rapor ediyorlar.Görsel Telif: Topology concept - Courtesy of Blue Brain Project
“Cebirsel topoloji aynı anda hem teleskop, hem de mikroskop görevi görebilir. Gizli yapıları (örneğin bir ormandaki ağaçları) görebilmek için ağ görüntülerini büyütebilir ve boş yerleri görebilir, hepsini aynı anda yapabilir,” diye açıklıyor Hess.
2015 yılında Mavi Beyin Projesi, beynin en fazla evrimleşmiş olan ve duyguların, eylemlerin ve bilincin merkezi olan neokorteksin bir parçasının dijital bir kopyasını yayınlamıştı. Bu son çalışmada cebirsel topoloji kullanılarak, keşfedilen çok boyutlu yapıların asla şans eseri oluşamayacağını göstermek amacıyla, sanal bir beyin dokusu üzerinde pek çok test gerçekleştirildi. Deneyler daha sonrasında Mavi Beyin Projesi’nin Lozan’da bulunan laboratuvarlarında gerçek beyin dokusu üzerinde gerçekleştirildi ve sonuçlar önceki sanal doku çalışmalarının biyolojik açıdan anlamlı olduğunu doğruladı ve beynin ağ gelişimi sırasında olabilecek en yüksek boyutlu yapılarla birlikte devamlı yeniden bir bağlanma süreci içerisinde olduğunu ortaya koydu.
Araştırmacılar sanal beyin dokusunu bir uyarıcıyla birlikte sunduğunda, yüksek boyutlardaki sinir takımları, bir an için araştırmacıların oyuklar olarak adlandırdığı yüksek yüksek boyutlu oyuklara yaklaşmak için birbirlerine bağlandılar. Beyin bilgileri işlerken bu yüksek boyutlu oyukların görünmesinin anlamı, ağdaki nöronların uyarıcıya karşı fazlasıyla organize bir bağlamda tepki veriyor olmasıdır. Bu, eğer beyin bir uyarana karşı yüksek boyutlu bloklardan bir kule inşa edip, ardından yıkarak tepki veriyorsa, beynin işe çubuklarla (1 boyutlu) başlayıp, sonra levhalar (2 boyutlu), sonra küpler (3 boyutlu), sonrasında ise 4, 5 ve daha fazla boyutlu karmaşık geometrilerle devam etmesine benziyor. Beyindeki aktivitenin ilerleyişi, kumdan yapılan bir kale inşa ediyor, ardından kale dağılıyor.
Araştırmacıların şimdi sormakta olduğu büyük soru ise, gerçekleştirebildiğimiz görevlerin karmaşıklığının, beynin inşa edebildiği bu çok boyutlu kumdan kalelerin karmaşıklığına bağlı olup olmadığı. Sinirbilim ayrıca, beynin anıları nerede sakladığı sorunuyla da boğuşuyor.
Topolojik dilde "boyut" sözcüğü karmaşıklığı tanımlamak için kullanılıyor. Singularity Hub’a konuşan, EPFL’den linsanüstü öğrencisi Max Nolte, “Çalışmamızda boyut sözcüğü, uzay boyutlarını tanımlamıyor; açıklamak istediğimiz geometrik nesnelerin topolojik boyutunu tanımlıyor. 7 veya 11 boyutlu simpleksler halen üç boyutlu fiziksel uzayda yerleşik olarak bulunuyor,” diyor. Yani burada boyut sözcüğü, simplekslerin karmaşıklığını anlatıyor.
Frontiers in Computational Neuroscience dergisinde yayımlanan makale, yapıların bir grup nöronun bir takım oluşturmasıyla açığa çıktığını gösteriyor. Her bir nöron, her bir diğer nörona, kesin bir geometrik nesne oluşturan spesifik bir şekilde bağlanıyor. Takımda ne kadar fazla nöron varsa, geometrik nesne o kadar fazla boyuta (karmaşıklığa) sahip oluyor. Beynin küçük bir parçasında 7 boyuta varan boyutlarda on milyonlarca böyle nesneler bulunuyor. Hatta bazı ağlarda, 11 boyutlu nesneler bile bulunabiliyor.
Bu keşif, beynin anlaşılmasının neden bu kadar zor olduğunu açıklayabilir. Sinirsel ağları çalışmak için uygulanan matematik, genellikle bu tür yüksek boyutlu geometrik nesneleri ve boşlukları tespit edemiyordu.
Eğer 4 boyutlu dünyalar bile zihnimizi bulandırıyorsa; 5, 6 ve daha yüksek boyutların pek çoğumuz için kavranması fazlasıyla karmaşıktır. İşte burada cebirsel topoloji devreye giriyor. Cebirsel topoloji, herhangi bir sayıdaki boyutları açıklamak için kullanılan matematik dalıdır. Cebirsel topolojiyi, beyin ağlarını çalışmak için kullanan matematikçileri, EPFL’den Kathryn Hess ve Aberdeen Üniversitesi’nden Ran Levi.
 Görsel, görüntülemeyecek bir şeyi göstermeye çalışıyor, çok boyutlu yapıların ve boşlukların evrenini. Sol tarafta, beynin en fazla evrimleşmiş parçası neokorteksin dijital bir kopyası yer alıyor. Sağ tarafta ise 1’den 7’ye kadar, hatta daha da fazla boyutlarda yapıları temsil etmeye çalışan değişik boyutlarda ve geometrilerde şekiller yer alıyor. Ortada yer alan “kara delik” çok boyutlu boşluklar yani oyuklar kompleksini sembolize etmek için kullanıldı. Mavi Beyin Projesi’ndeki araştırmacılar son makalelerinde, bu tür oyuklara bağlanan nöron gruplarının, sinirsel yapılar ve işlevler arasındaki kayıp bağlantıyı sağladığını rapor ediyorlar.
Görsel, görüntülemeyecek bir şeyi göstermeye çalışıyor, çok boyutlu yapıların ve boşlukların evrenini. Sol tarafta, beynin en fazla evrimleşmiş parçası neokorteksin dijital bir kopyası yer alıyor. Sağ tarafta ise 1’den 7’ye kadar, hatta daha da fazla boyutlarda yapıları temsil etmeye çalışan değişik boyutlarda ve geometrilerde şekiller yer alıyor. Ortada yer alan “kara delik” çok boyutlu boşluklar yani oyuklar kompleksini sembolize etmek için kullanıldı. Mavi Beyin Projesi’ndeki araştırmacılar son makalelerinde, bu tür oyuklara bağlanan nöron gruplarının, sinirsel yapılar ve işlevler arasındaki kayıp bağlantıyı sağladığını rapor ediyorlar.Görsel Telif: Topology concept - Courtesy of Blue Brain Project Görsel, görüntülemeyecek bir şeyi göstermeye çalışıyor, çok boyutlu yapıların ve boşlukların evrenini. Sol tarafta, beynin en fazla evrimleşmiş parçası neokorteksin dijital bir kopyası yer alıyor. Sağ tarafta ise 1’den 7’ye kadar, hatta daha da fazla boyutlarda yapıları temsil etmeye çalışan değişik boyutlarda ve geometrilerde şekiller yer alıyor. Ortada yer alan “kara delik” çok boyutlu boşluklar yani oyuklar kompleksini sembolize etmek için kullanıldı. Mavi Beyin Projesi’ndeki araştırmacılar son makalelerinde, bu tür oyuklara bağlanan nöron gruplarının, sinirsel yapılar ve işlevler arasındaki kayıp bağlantıyı sağladığını rapor ediyorlar.Görsel Telif: Topology concept - Courtesy of Blue Brain Project
“Cebirsel topoloji aynı anda hem teleskop, hem de mikroskop görevi görebilir. Gizli yapıları (örneğin bir ormandaki ağaçları) görebilmek için ağ görüntülerini büyütebilir ve boş yerleri görebilir, hepsini aynı anda yapabilir,” diye açıklıyor Hess.
2015 yılında Mavi Beyin Projesi, beynin en fazla evrimleşmiş olan ve duyguların, eylemlerin ve bilincin merkezi olan neokorteksin bir parçasının dijital bir kopyasını yayınlamıştı. Bu son çalışmada cebirsel topoloji kullanılarak, keşfedilen çok boyutlu yapıların asla şans eseri oluşamayacağını göstermek amacıyla, sanal bir beyin dokusu üzerinde pek çok test gerçekleştirildi. Deneyler daha sonrasında Mavi Beyin Projesi’nin Lozan’da bulunan laboratuvarlarında gerçek beyin dokusu üzerinde gerçekleştirildi ve sonuçlar önceki sanal doku çalışmalarının biyolojik açıdan anlamlı olduğunu doğruladı ve beynin ağ gelişimi sırasında olabilecek en yüksek boyutlu yapılarla birlikte devamlı yeniden bir bağlanma süreci içerisinde olduğunu ortaya koydu.
Araştırmacılar sanal beyin dokusunu bir uyarıcıyla birlikte sunduğunda, yüksek boyutlardaki sinir takımları, bir an için araştırmacıların oyuklar olarak adlandırdığı yüksek yüksek boyutlu oyuklara yaklaşmak için birbirlerine bağlandılar. Beyin bilgileri işlerken bu yüksek boyutlu oyukların görünmesinin anlamı, ağdaki nöronların uyarıcıya karşı fazlasıyla organize bir bağlamda tepki veriyor olmasıdır. Bu, eğer beyin bir uyarana karşı yüksek boyutlu bloklardan bir kule inşa edip, ardından yıkarak tepki veriyorsa, beynin işe çubuklarla (1 boyutlu) başlayıp, sonra levhalar (2 boyutlu), sonra küpler (3 boyutlu), sonrasında ise 4, 5 ve daha fazla boyutlu karmaşık geometrilerle devam etmesine benziyor. Beyindeki aktivitenin ilerleyişi, kumdan yapılan bir kale inşa ediyor, ardından kale dağılıyor.
Araştırmacıların şimdi sormakta olduğu büyük soru ise, gerçekleştirebildiğimiz görevlerin karmaşıklığının, beynin inşa edebildiği bu çok boyutlu kumdan kalelerin karmaşıklığına bağlı olup olmadığı. Sinirbilim ayrıca, beynin anıları nerede sakladığı sorunuyla da boğuşuyor.
Kaynak ve İleri Okuma
- Frontiers. "'Multi-dimensional universe' in brain networks: Using mathematics in a novel way in neuroscience, scientists demonstrate that the brain operates on many dimensions, not just the 3 dimensions that we are accustomed to." ScienceDaily. ScienceDaily, 12 June 2017. https://www.sciencedaily.com/releases/2017/06/170612094100.htm
- Cliques of Neurons Bound into Cavities Provide a Missing Link between Structure and Function http://journal.frontiersin.org/article/10.3389/fncom.2017.00048/full > DOI: 10.3389/fncom.2017.00048
- Is There a Multidimensional Mathematical World Hidden in the Brain’s Computation?";
Etiket
Projelerimizde bize destek olmak ister misiniz?
Dilediğiniz miktarda aylık veya tek seferlik bağış yapabilirsiniz.
Destek Ol
Yorum Yap (0)
Bunlar da İlginizi Çekebilir
06 Kasım 2014
Nöron Ölümünün Sorumlusu Amiloid Beta Değil, Amiloid Tau
01 Temmuz 2015
Gerçek İşlevli Yapay Nöron Üretildi