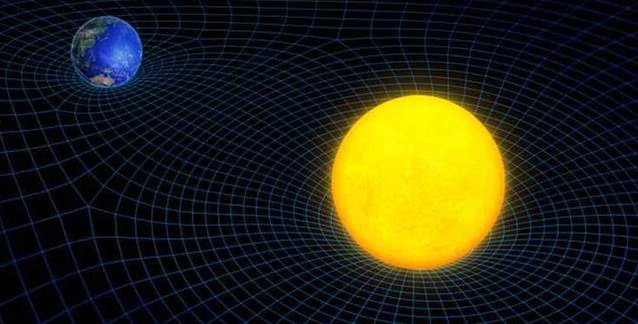
Genel görelilik kuramının uzay-zaman modeli, eşdeğerlik ilkesinin özel görelilik kuramı çerçevesinde yorumlanması ile ortaya çıkan ve çarpık bir geometriyle modellenebilen soyut bir dokudur. Bu çarpık –veya eğri- doku, kütleçekimini açıklamaktadır: Kütleçekim kuvveti denilen olgu, uzay-zamanın eğriliğidir. Yani, aslında böyle bir kuvvet yoktur. Yanlış anlamadınız veya biz yanlış bir şey söylemedik. Bu sizi şaşırtmadıysa eğer sorun değil, yazımız bittiğinde bu duyguyu tadacağınızı umuyoruz. :) Genel görelilik yolculuğumuza hoş geldiniz.Bu yazımızda da tıpkı önceki yazımızda (Kuantum Teorisine Genel bir Bakış) olduğu gibi konuya bütünsel bir bakış açısı getirecek ve geçtiğimiz yüzyılın en önemli bilimsel devrimlerinden biri olan gene görelilik kuramını genele hitap eden bir dil yaklaşımla ele almaya çalışacağız. Bu yüzden acele etmeden, olguları dikkatli ve açık bir şekilde ifade etmeye çalışacağız. Umarız ki, herkes için faydalı olur. Yazımızı kendi içerisinde beş bölüme ayırdık. İlk dört bölüm esas konumuzu işlemek yani genel görelilik kuramını anlayabilmek için önemli gördüğümüz temel konuları içermektedir. Son bölümde ise esas konumuzu ele alıp noktayı koyacağız. Yazımızın bölümleri şöyle:

1. Eşdeğerlik ilkesi
2. Boyutlar ve hareket
3. Özel görelilik kuramına genel bir bakış
4. Öklid-dışı geometriler
5. Genel görelilik kuramının inşası ve sonuçları

Hazır mısınız? Hadi o zaman, başlayalım...

1. Bölüm: Eşdeğerlik İlkesi

Yazımızın giriş cümlesinde kullandığımız ve kuramın özünde yatan kavrayış olması nedeniyle “eşdeğerlik ilkesi nedir?” sorusu ile giriş yapalım.Özlü cevabımız şudur; eşdeğerlik ilkesine göre ivmeli hareket ile kütleçekim kuvveti dediğimiz fenomen aynı madalyonun iki ayrı yüzü gibidir, fiziksel sonuçları birbirinden ayırt edilemez. Biraz açarsak, eşdeğerlik ilkesine göre;a) Kütleçekimsiz alandaki ivmeli hareket, yerel olarak gerçek bir kütleçekimsel alandan ayırt edilemez. Başka bir deyişle ivmeli hareket kütleçekimini “taklit eder”.b) Bir kütleçekim alanında serbest düşme halinde, kütleçekim etkisi yerel olarak hissedilmez.

Bu iki maddeyi bir örnek üzerinde anlamaya çalışalım mı?

Beşiğinde uyumakta olan bebek yerel bir kütleçekim alanına tabidir: Dünyanın kütleçekimi. Bu da bebeğimizin, sırtında "ağırlık" dediğimiz bir kuvvetin oluşmasına yol açar. Bebek bu kuvveti "hissetmektedir". Ya da bebek kendi ağırlığının "farkındadır".

Şimdi kütleçekimi olmayan bir ortam düşünelim. Burası yıldızlardan ve her şeyden uzak, boş bir uzay olsun. Şimdi bebeğimiz bu boş yani kütleçekimsiz uzayda hızlanarak hareket eden bir aracın içinde, beşiğinde uyuyor olsun. Bebek sırtında yine bir kuvvet ya da diğer deyişle ağırlığını hisseder miydi? Sezgisel olarak hissedeceğini düşünebilirsiniz ki; haklısınız da. Hatta bunun üzerine biraz düşünecek olursanız günlük hayatımızda sıkça deneyimlediğimiz, ivmeli hareketten kaynaklanan ağırlık kuvveti değişimini fark edebiliriz. Uçak kalkış için hızlanırken sırtınız koltuğa yapışır ve sırt bölgesinde hissettiğiniz ağırlığınızın giderek arttığını deneyimleriz. Ya da asansör yukarı çıkmak üzere hareketlendiği ilk anda ayak tabanlarınızda kendi ağırlığınızdan biraz daha fazla yük hissedersiniz. Tersi de geçerlidir: aşağı inmek üzere hareketlendiği ilk anda anlık bir hafifleme duygusu hissedersiniz, ağırlığınız biraz azalmıştır. Ta ki asansörün hızı sabit bir değere ulaşana dek. Bu örnekle a) maddesinin fiziksel anlamını öğrendik: Bebek beşiğinde uyuyor iken hissettiği ağırlık kuvvetinin gerçek bir kütleçekim alanından mı (dünya) yoksa kütleçekimsiz bir uzayda ivmeli olarak hareket ediyor olmasından mı kaynaklandığını ayırt edemez. Her iki durumun da fiziksel sonuçları aynıdır.

Peki b) maddesi bize ne söyler? Onu da şöyle açıklayalım; Bir uçakta seyahat halindesiniz. Dünyanın kütleçekim alanına tabi olduğunuzdan koltuğunuzda oturabiliyor, kahvenizi yudumlayıp derginizi okuyabiliyorsunuz. Biraz tatsız bir durum ama, uçağın motorları duruyor ve uçak hızla irtifa kaybetmeye başlıyor. Şimdi kabinin içinde olanları hayal etmeye çalışın. Kabinde emniyet kemerini bağlamamış yolcular ve bir yere sabitlenmemiş bütün nesneler kabinin içinde sanki kütleçekimsiz bir ortamdaymışçasına “yüzerlerdi” değil mi? Zaten yörüngedeki uzay istasyonlarında da aynı şey olmakta: istasyon dünyaya serbest düşmektedir ve bu yüzden içindeki astronotlar kabinde serbestçe yüzmektedirler: kütleçekimsiz ortamda oldukları için değil, bir kütleçekim alanında serbest düştükleri için! Belki konu dışı olacak ama içinizden şu soru geçmiş olabilir: Madem istasyon serbest düşüyor, neden kısa bir süre sonra dünyaya çarpmıyor? Cevabımız ferahlatıcı: öyle yüksek -ve sürekli sabit tutulan- bir hızla yörüngede dönmektedir ki, düşmesi, dünya yüzeyine dik değil, paralel olarak gerçekleşmektedir. Bu “paralel serbest düşme” istasyonun nerdeyse hep aynı irtifada kalmasına neden olmaktadır.

Bu örnekle b) bendini de anlamış bulunuyoruz: Bir kütleçekim alanında serbest düşme hareketi (ki, bu bir ivmeli harekettir) yerel olarak (uçağın içi) hissedilmez; sanki kütleçekimi yok gibidir!

Einstein'in 8 yıl boyunca geceli gündüzlü çalışıp genel görelilikle meyvesini veren çalışmasının temel çıkış noktası işte budur; ivmeli hareket ile kütleçekim kuvveti dediğimiz fenomen arasında güçlü ve ayırt edilemez bir benzerlik var. Her iki durumda da yerel sistemde yapılacak deneyler sonucu değiştirmeyecektir. Yani deney düzeneği ister gerçek kütleçekimine maruz kalsın, isterse artan ivmeli hareket durumunda olan yerel bir sistemde olsun her iki deneyde de elde edilen sonuç aynı olacaktır. Burada özellikle uzman okurların fark etmiş olabileceği bir husus için küçük bir parantez açalım. Deney sonucunun aynı olması ivmenin belli bir değerde olmasını gerektirir. Ne biraz eksik, ne de biraz fazla. Tam da kütleçekim kuvvetinin büyüklüğüne tekabül edecek miktarda!

Albert Einstein burada sizlere anlatılanlardan yola çıkarak "Madem öyle, Ben ivmeli hareketin doğası üzerinden ilerleyerek kütleçekimin mekanizmasını aydınlatabilirim" dedi. Ancak henüz bu işe girişecek durumda değiliz. Halletmemiz gereken işlerimiz var. Şimdi bu bölümün ikinci kısmı ile devam edelim.

2. Bölüm: Boyutlar ve Hareket

Evrenimize baktığımızda bütün gözlemlenebilir maddeler için ölçülebilir en fazla üç yönelim olduğunu görebiliyoruz: Genişlik, yükseklik ve derinlik. Peki neden daha fazla değil? Bu soruya aslında cevap verdik: “ölçülebilir” kelimesini kullandık, cevap da zaten bu kelimenin içinde saklı. Kimse daha fazla boyut yoktur deme cesaretini gösteremez, kaldı ki yeni nesil fizik kuramları daha fazla boyutların kaçınılmaz olduğunu ortaya koyuyor. Yalnız küçük bir pürüz var; bu “ekstra boyutlar” şu anda ölçümlerimize konu olamayacak kadar küçük bir dünyada titreşen, kaynayan ilmekler ve parçacıklar için “görülebilir” olduğu varsayılıyor.

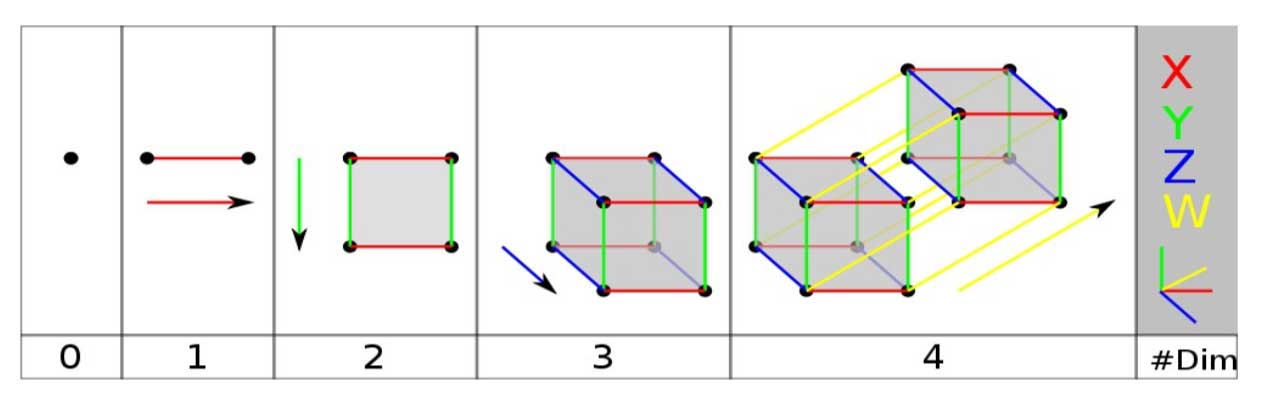Nokta boyutsuz olarak kabul edilmektedir (0). Bir noktanın uzayda herhangi bir yöndeki hareketi, tek boyutlu bir doğru ifade eder (1). Doğrunun farklı bir yönde hareketi iki boyutlu bir yüzeyi meydana getirir (2). Yüzeyin üçüncü farklı bir yöne hareketi ise uzayda üç boyutlu bir uzayı, yani hacimsel bir bölgeyi oluşturur (3). Bu işlem her defasında farklı yönlerde tekrarlanarak ekstra boyutlar elde edilebilir (4).

Sıkça yapılan bir benzetmeyle ifade edecek olursak, bir ip bize tek boyutlu gibi görünür, hatta ölçüm aletlerimiz yeterince duyarlı değilse bunu doğrulayacaktır. Ancak ipin üzerinde yürümekte olan bir karınca için işler biraz farklıdır.

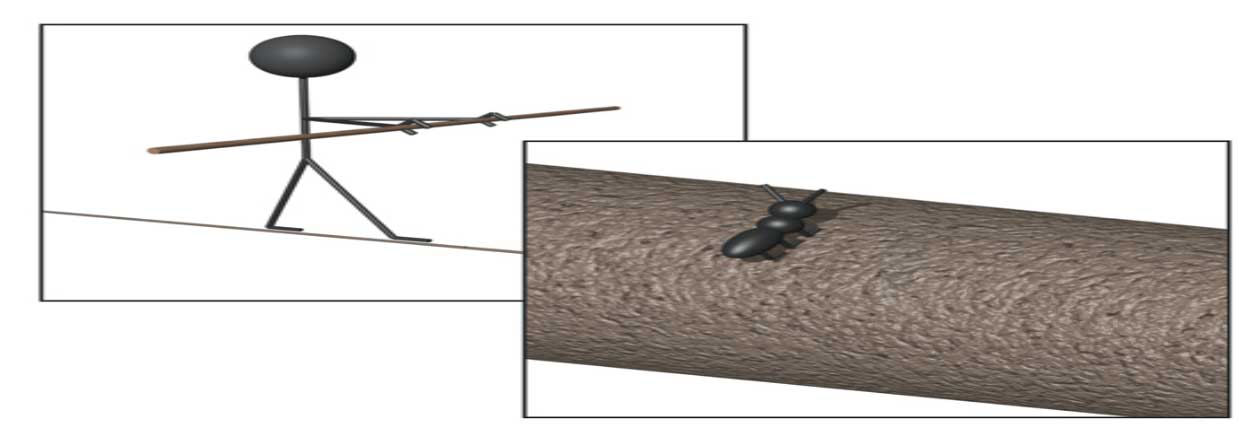Bir ip üzerinde yürüyen cambaz için ip tek boyutlu gibi görünür. Ancak, ip üzerinde yürüyen karınca için durum hiç de öyle değildir: İpin uzayda birden fazla yönelimi vardır, yani ip, birden fazla boyuta sahiptir.

O halde boyut konusu tamamen bir “ölçek” konusudur. Genel Görelilik kuramı makroskopik cisimlerin kütleçekimsel doğasını incelediğinden ve makroskopik cisimler ölçülebilir üç uzamsal boyuta sahip olduklarından bize bu kuramın tarifi için üç uzamsal boyut yeterlidir. Bu sınırlama bize genel görelilik kuramının neden kuantum düzeyinde kütleçekimini açıklamakta yetersiz olduğunu açıklayabilir. Başka sebepleri de olmakla birlikte, ekstra boyutlar genel görelilik kuramının fiziksel çatısı altında bizi anlamlı bir sonuca götürmez.

Peki, uzamsal üç boyut dışında başka boyutlar var mıdır? Mesela uzamsal boyutları üçlü koordinat sisteminde tanımlayabilir ve herhangi iki nokta arasında “yer değiştirebiliriz”. Acaba yer değiştirdiğimiz başka bir boyut daha var mıdır? Muhtemelen tahmin ettiniz: Zaman.

Evrende bulunan her şey zamanda hareket eder, hatta en doğru deyişle uzay-zamanda yer değiştirir. Burada uzay-zaman ifadesi, üç uzamsal boyut (x, y, z) ile bir zaman boyutunun (t) birlikteliğini ifade etmektedir. Bu birliktelik, evrende her şeyi dört boyutlu soyut bir uzay-zaman dokusuna hapseder. Çünkü kaçınılmaz olarak her şey bu dokuda yer değiştirmektedir. Hareketin, bu boyutlarla ifade edilebilen uzay-zaman noktaları (t, x, y, z) arasında gerçekleştiğini düşüneceğiz.

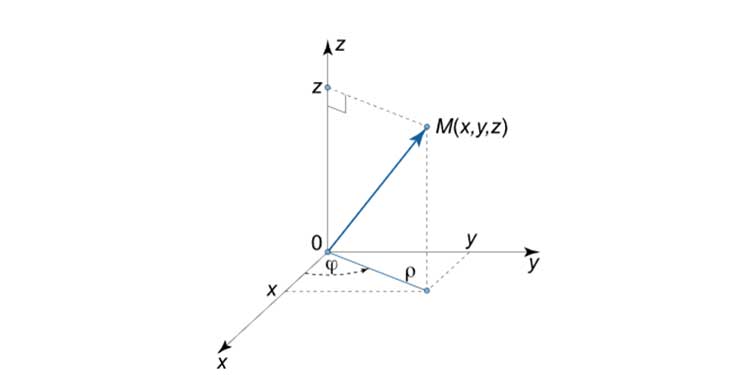Uzay-zamanda bir noktanın uzamsal konumu üç boyutlu bir koordinat sisteminde M(x, y, z) biçiminde tanımlanabilir.

Yukarıda uzay-zamanda bir noktanın uzamsal koordinatlarını M(x, y, z) görüyoruz. Peki, zaman boyutunu nasıl dahil edeceğiz?

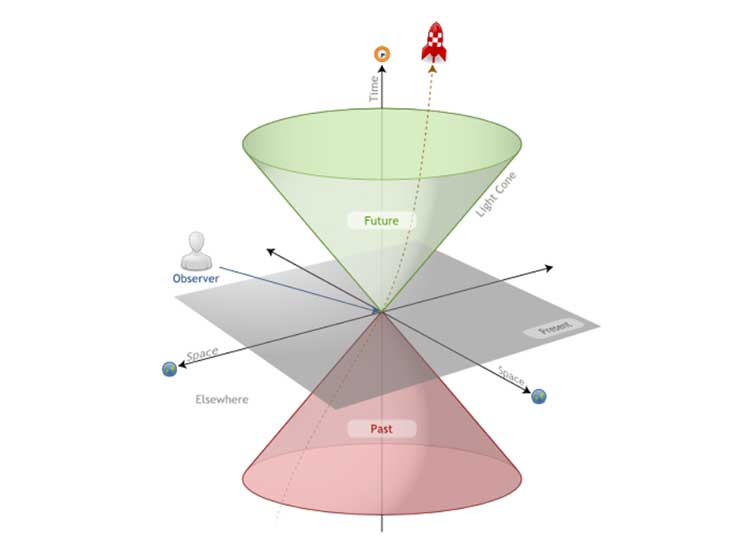
Üç uzamsal boyutu tek bir eksen (space) olarak düşünürsek, zaman boyutunu (time) bu eksene dik bir şekilde yerleştirebiliriz. Gözlemcinin (observer) “şimdiki an” da gözlemlediği herhangi bir olay iki eksenin çakıştığı noktada yani konilerin tepe noktalarının buluştuğu yerde gösterilebilir. Grafiğimize göre bu olay, bir roketin kalkış anını göstermektedir. Present olarak adlandırılan uzay-zaman düzlemi üzerinde bulunan bütün noktalarda yaşanan olaylar, farklı yerlerde eş anlı olarak gerçekleşen olaylardır. Örneğin bir P olayının koordinatları uzay-zamanda present düzlemi üzerinde ise, P olayı ile roketin kalkışının aynı anda gerçekleştiğini söyleyebiliriz. Her iki olayın da zaman boyutunun (t) koordinatı aynıdır. Farklı olan uzamsal (space) koordinatlarıdır (x, y, z). Peki olayın geçmiş ve geleceğine ait uzay-zaman koordinatları neden bir koni biçiminde? Bu sorunun cevabı ışık hızının bir limiti olmasından dolayıdır. Bir sonraki bölümde bu konuyu ele alacağız ancak kısaca söylemek gerekirse, olmuş bir olayın bilgisi ışık hızıyla evrene yayılmaktadır. Dolayısıyla zamanda geriye yani geçmişe doğru gittikçe, olayınbilgisi daha geniş bir alana yayılmış olmalıdır ve koninin aşağı doğru genişlemesi gerekir. Gelecek konisi ise aynı mantıkla açıklanabilir. “Şimdi” gerçekleşen bir olayın geleceğe yansıması, ışık hızının belirlediği sınırlardan dışarı taşamaz. Zamanda ileri doğru gittikçe olayın etkisi giderek genişleyen ancak bir sınırdan ötesine geçemeyen bir uzay-zaman bölgesi içerisinde ele alınmalıdır. Örneğin roketimizin kalkışından sonraki geleceği, yani uzay-zamanda hareketi, gelecek konisi içerisinde gerçekleşir. Bu sınırlama kuantum yazımızdan hatırlayacağınız gibi yerellik (locality) olgusunu çağrıştırmaktadır: Bir olay, belli bir zaman dilimi içerisinde fizik yasalarınca sınırlanan belli bir bölge içerisinde etkisini göstermek zorundadır. Madem konuyu açtık, kuantum dolaşıklığın yerelliği ihlal ettiğini hatırlamış olalım.

Artık uzay-zamanda nasıl koordinat verebileceğimizi biliyoruz. Örneğin yörüngede dönmekte olan bir uydunun belli bir anda uzamsal koordinatları (x, y, z) olsun. Ancak işe zamanı da dahil etmemiz gerektiğini öğrendik, bu yüzden uydunun uzay-zaman koordinatlarını vermemiz gerekirse: (t, x, y, z) olacaktır.

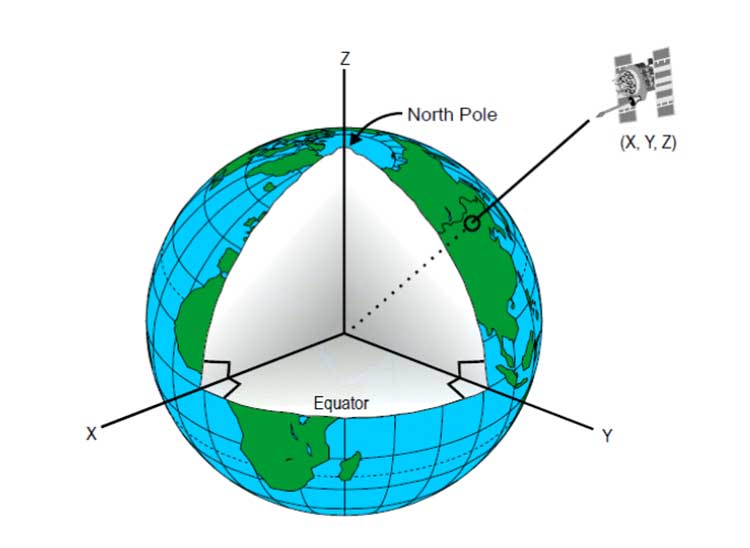Üçlü uzamsal koordinat sisteminde kartezyen eksenlerin kesim noktası (0,0,0) cismin merkezine alınır.

Yörüngesinde dönmekte olan bir uydunun iki uzay-zaman noktası arasındaki yer değiştirmesi vektörel yani belli bir yöne sahip fiziksel büyüklük olarak ifade edilebilir. Şimdi konunun kalbine yaklaşıyoruz. Uydu, yörüngesinde sabit bir hızla dönmekte iken birim zaman aralıklarında uzaydaki yer değiştirme miktarları eşittir. Yer değiştime vektörünün yönüne bağlı olarak hareketin uzamsal boyutlara dağılım miktarı değişebilir. Örneğin belli bir anda sadece x ve y eksenlerinin oluşturduğu düzlem (ekvator) üzerinde hareket edebilir veya yine belli bir anda sadece y-z veya x-z eksenlerinin oluşturduğu düzlem (boylam) üzerinde hareket edebilir veya her üç eksende de hareket edebilir.

Yukarıdaki şekle dikkat edin; ekvatoral dönüşlerde uzay-zaman koordinatlarının (t, x, y, 0) biçiminde, boylamsal dönüşlerde (t, 0, y, z) veya (t, x, 0, z) biçiminde ve diğer bütün dönüşler ise dört eksende birden (t, x, y, z) ifade edilmesi gerekir. İyi de bütün bunların anlamı nedir? Şu; uydunun hareketinin yönüne bağlı olarak uzay-zaman boyutlarının her birinde gerçekleşen yer değiştirme miktarları değişmekte ancak hepsinin toplam (bileşke) yer değiştirmesi sabit kalmaktadır. Yani yukarıya yazdığımız dört farklı kombinasyonda da birim zamanda toplam yer değiştirme miktarı aynı (bileşke vektörler) ancak bu yer değiştirmelerin boyutlara dağılımı farklıdır (izdüşüm vektörleri) Bu farklılık, her bir boyuta düşen hareket miktarının değişken olduğu anlamına gelir. Basitçe bir örnek ile, iki kişi aynı hızla biri kuzeye diğeri kuzeydoğuya olacak şekilde aynı noktadan yürümeye başlasınlar. İkisinin de birim zaman içinde uzay-zamanda yer değiştirme miktarları eşittir. Ancak birisi hareketinin tamamını kuzey yönüne harcarken diğeri hem kuzey hem de doğu yönüne harcamaktadır. Dolayısıyla kuzeydoğuya yürüyen kişinin birim zamanda kuzey istikametinde kat ettiği yol daha az olacaktır. Çünkü toplam hareketinin bir kısmı doğu ekseninde gerçekleşmektedir.

Fark ettiyseniz yukarıdaki örnekte zaman boyutunu uzamsal boyutlardan bağımsız, hareketin yönü ve büyüklüğünden etkilenmeyen, sabit bir boyut gibi ele aldık. Toplam hareketin üç uzamsal boyut arasında değişken miktarlarda dağılabildiğini gördük, peki neden dördüncü boyut olan zamandaki hareketin büyüklüğü de değişken olmasın? Örneğin hareketin tamamı zamanda gerçekleşemez mi? Çünkü biliyoruz ki zaman da aslında bir hareket ölçüsü, yer değiştirilebilir bir boyut, uzay-zamanın ayrılmaz ve ona içkin bir boyutudur. Şimdi, ima ettiğimiz şey zamanın evrenin her köşesinde sabit bir hızla akmadığı, aksine bazı özel durumlarda tik-tak aralığın değişken olduğudur. Buna hazırlıksız yakalandığınızı düşünüyorsanız dert etmeyin. Özel görelilik kuramının sularında yelken açıp konuya yakından bir göz atalım.

3. Bölüm: Özel Görelilik Kuramına Genel Bir Bakış

Özel görelilik kuramı Einstein tarafından 1905 yılında yayınlanmış ve insanoğlunun o güne dek zaman ve hareketin doğası hakkında bildiği her şeyi kökünden değiştirmiştir. Einstein, bu kuramın devrimsel sonuçlarını kütleçekim problemine uygulayarak 10 yıl sonra , 1915’te ikinci büyük devrimi gerçekleştirecekti. Özel göreliliği anlayamadan genel göreliliği anlayamayız. Bu yüzden bu kuramın anlatımında teknik bir dil kullanmak yerine sezgisel olarak kavranmasına önem verecek şekilde sözel bir anlatım kullanacağız.Özel görelilik kuramı bize ne anlatır? Bizi bu yazımızda daha çok ilgilendiren şu iki şeyi:Hareketin göreliliği: Evrende mutlak hareketsizlik yoktur. Bir cismin hareketi veya hareketsizliği hakkında konuşuyor isek bunu seçilen bir referans noktasına göre yapıyoruzdur. Ancak bu değişken durum fizik yasalarının işleyişini değiştirmez: Hangi özel referans sistemini ele alırsak alalım, fizik yasaları hepsinde de aynı derecede geçerlidir.

Işığın hızı sabittir: Işık hızı gözlemcilerin veya kaynağının hareketinden bağımsız olarak her yöne aynı hızla yayılır. Ayrıca hiçbir şey ışıktan daha hızlı hareket edemez.

Şimdi bu iki temel varsayımdan ilkini biraz açalım. Evrende mutlak hareketsizlik yoktur dedik. Örneğin otomobilinizin kadranında 90km/h görüyor iseniz, bu değer “yere göredir”. Peki sizinle aynı süratle aynı yöne doğru gitmekte olan bir başka otomobilde bulunan meraklı bir çocuk hızınızı kendi içinde bulunduğu arabaya göre ölçseydi ne bulurdu? Evet, sıfır bulurdu. Bu durumda siz hareketli misiniz hareketsiz mi? Cevap; bunun seçilen referansa (yer veya çocuk) göre değişeceğidir. Şimdi bu açıklamadan tatmin olmayanlarınız olabilir. Onlar, “nihayetinde çocuk eğer ölçtüğü arabanın dönen tekerleğine baksaydı veya şoförü ile iletişim kurabilmiş olsaydı, hareketli olduğunu anlayacaktı” diyebilirler. Haklılar da. Ancak uzay boşluğundaki hareket için ne diyeceğiz peki? Kendinizi bir an için uzay boşluğunda süzülen bir astronot olarak hayal edin. Yanınızdan hızla bir meteor gelip geçti. Sonra merak edip döndünüz ve geçip giden meteorun hızını ölçtünüz: saniyede 3,5 km. Sonra bir anda kafanızın içinde bir yıldırım çaktı. Ya aslında o meteor boşlukta öylece asılı duruyorsa ve gerçekte saniyede 3,5 km hızla onun yanından geçip giden ben isem? Hatta işi daha da ileri götürebilir, sizin hızınızın saniyede 1,5 km, tam arkanızdan size yaklaşan ve sizinle aynı doğrultuda hareket eden meteorun hızının ise saniyede 5 km olduğunu söyleyebilir, bu koşullarda meteorun hızını yine 5-1,5= 3,5 km/saniye olarak bulacağınızı hatırlatabiliriz.. Bu ihtimalleri çürütülemeyecek şekilde sonsuza dek sıralayabiliriz, bizi kim durdurabilir? Şimdi bu yükün altından kalkabilecek misiniz? O yüzden şunu varsayacağız; “Evrende mutlak hareketsizlik yoktur”.

İkinci konu ile devam edelim, ışık hızı neden sabittir ve bunun kuram açısından sonuçları nelerdir? Işık hızının sabitliği kuramdan önce bilinmekteydi. James Clerk Maxwell 19.yy ortalarında elektrik ve manyetik alan kuvvetlerinin aynı madalyonun iki yüzü olduğunu fark etmiş ve bu iki kuvveti birleştirerek “elektromanyetik teoriyi” kurmuştur. Teorinin formülasyonu elektromanyetik dalgaların (ışık) sabit ve sonlu değerde bir hızla yayılması gerektiğini göstermiştir. Ancak büyük bir sorun vardı. O güne dek harekete dair bilinenlere göre ışık hızı sabit olamazdı. Örneğin yerdeki bir gözlemci ileri doğru bir el feneri tuttuğunda ışık c hızıyla yol alıyorsa, bu gözlemci v hızıyla hareket eden bir trene binip yine aynı yöne doğru el fenerini tuttuğunda ışık yerdeki bir gözlemciye göre v+c hızıyla yol almalıydı. Örnek verecek olursak; saatte 30 km hızla giden bir otomobilin içinden ileri doğru saatte 100 km hızla bir tenis topu fırlatırsak, top arabadan yere göre saatte 130 km hızla ayrılır. O halde ışık hızı nasıl sabit olabilirdi ki? Işık sonsuz bir hızla yayılıyor olsaydı çatışma çözülürdü. Fener ışığı örneğinde sonsuz ışık hızı ile sonlu tren hızını toplar, yine sonsuz elde ederdik ve iş tatlıya bağlanırdı.

Bilim tarihi incelendiğinde bu tür çatışmaları önemli bilimsel gelişmelerin takip ettiği görülebilir. İşte, özel görelilik kuramı da bunlardan biridir. Bizi bu kurama götüren önemli kilometre taşlarından biri de 1887’de Albert Michelson ve Edward Morley tarafından yapılan Michelson-Morley deneyidir. Deney, hareketten bağımsız olarak ışık hızının her yönde aynı olduğunu ortaya koymuştur.

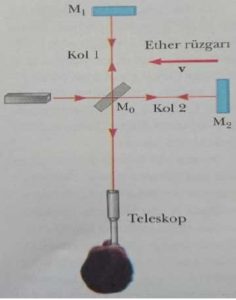Sağ tarafta bulunan deneyi kısaca özetlemek gerekirse, bir kaynaktan yola çıkıp yarı geçirgen bir aynada (M 0 ) birbiriyle 90 birbiriyle dik açı yapacak şekilde iki kola ayrılan ışınlar aynalardan (M 1 ve M 2 ) yansıyıp geri dönerler. Şayet esir varsa ve resimde gösterildiği gibi bir yöne doğru v hızıyla hareket ediyorsa aynalardan yansıyıp dönen ışınların hızı birbirinden farklı olacaktır. Tıpkı akıntıya karşı veya akıntı yönünde yüzmenin, yüzme hızınızı etkilediği gibi. Ancak sonuç beklendiği gibi olmadı. Her iki koldan yansıyıp gelen ışınlar dedektöre (görselde teleskopun yeri) eşit sürede varmıştı. Farklı olsaydı, yıkıcı bir girişim deseni yani yansıyıp dönen ışınların birbirini iptal etmesi beklenirdi. O halde iki seçeneğimiz var: Ya dünya hareketsizdir, ya da esir yoktur. İlk seçeneği tartışmaya gerek olmadığına göre esir yoktur. Sonucu genişletirsek, ışık her yöne doğru aynı hızla yayılmaktadır. Kaynağın veya gözlemcilerin göreli hareketinin ışığın hızına bir etkisi yoktur.

Varılan bu sonuç mutlak bir kavramın esnetilmesini gerektiriyordu: ZAMAN. Zamanın esnemesi yani, tik-tak aralığının uzaması veya kısalması fikri baş döndürücü görünüyor. Peki bu nasıl oluyor? Kemerlerinizi bağlayın ve dikkatle okumaya devam edin.

Işık hızının %99’u (0,99c) hızla giden bir trenin içindesiniz. Elinizde bir fener var. Trenin hareket ettiği yöne doğru fenerinizi tutup düğmesine basıyorsunuz. Bir ışık huzmesinin ileri doğru gittiğini, trenin önünü aydınlattığını görüyorsunuz. Görmekle yetinmeyin, onu ölçün de: “c”. İyi de tren 0,99c hızıyla gitmiyor muydu? Işık hızını c olarak ölçtük, tren de 0,99c idi; o halde ışık yerdeki birisine göre 1,99c hızla mı gidiyor olacaktır? Bu ise imkansız, yerdeki gözlemci de fener ışığının c hızıyla yol aldığını görmek zorunda.

Bu çatışmayı çözebilmenin tek bir yolu var: Aslında fenerden çıkan ışık trene göre 0,01 c hızıyla yol almakta ancak siz onun sizden, yani trene göre c hızıyla uzaklaştığını ölçmektesiniz! Dolayısıyla yerdeki gözlemci ile mutabık kalıyorsunuz :). Hem bu çözüm yerdeki gözlemci için de uygun: trenin içinde 0,01c hızla giden bir ışık huzmesi var, trenin hızı da 0,99 c olduğuna göre ışığın hızı ikisinin toplamı yani c olur. İyi ama nasıl oluyor da trene göre 0,01c hızla giden ışık huzmesi trenin içindeki birisi tarafından c hızı ile gidiyormuş gibi ölçülüyor? İşte yukarıda bahsettiğimiz noktaya geldik şimdi: Zaman genişlemesi! Kolunuzdaki saatin tik-tak aralıkları yerdeki gözlemcinin saatinin tik-tak aralığına göre daha geniş. Yani sizin zamanınız yerdeki gözlemcinin zamanına göre daha yavaş akıyor! Ancak bu şekilde olursa ışık hızının değişmezliği konusunda yerdeki gözlemciyle mutabık kalabiliyorsunuz! Zamanın genişlemesi!

Çatışmanın çözümüne başka bir açıdan bakalım: Bir tenis topu fırlatma makinesi üreticisi makinesinin kusursuz olduğunu iddia etmektedir; öyle ki bu makine evrenin neresine götürülürse götürülsün, hareket durumu ne olursa olsun tenis toplarını hep aynı hızla fırlatıyor: tam 20 metre/saniye! Burada tenis topunun hızının değişmezliği ışık hızının sabitliğini temsil etmektedir. Şimdi size ve bana topun hızını ölçüp teyit edebilmemiz için tıpatıp aynı birer saat veriliyor olsun. Ayrıca ölçüm süremiz 10 saniye olsun kesinlikle ne az ne de fazla, yani topun havada tam 10 saniye boyunca kat ettiği yolu hesaplayacağız. Siz ölçümünüzü ultra yüksek hızlı bir trenin içinde ben ise yerde yapacağım. Şimdi makineyi yanınıza alıp treninize binebilirsiniz. Bulunduğunuz tren öyle yüksek bir hızla hareket ediyor olsun ki, kolunuzdaki saat yerdeki benim saatime göre 2 kat yavaş işliyor olsun. İlk ölçümü ben yapıyorum ve 10 saniye içinde topun 200 metre yol aldığını hesaplıyorum. Ardından topun hızını hesaplıyorum: 200metre/10saniye= 20metre/saniye. Harika, tam da olması gerektiği gibi! Şimdi sıra sizde. Topu fırlatıyorsunuz ve bizim saatimize göre yine 10 saniye geçiyor. Ancak trenin içinde zaman yere göre 2 kat yavaş işlediği için sizin saatinize göre henüz 5 saniye geçmiş olmalıdır. Ancak kural gereği benim saatime göre ölçümünüzü sonlandırmak zorundasınız. Sizin kolunuzdaki saate göre ölçümünüz 5 saniye sürmüş, bu süre zarfında topun hareket hızı da trenin içerisindeki diğer her şey gibi 2 kat yavaşladığı için top 200 metrenin yarısı kadar yani 100 metre yol kat etmiştir. Hadi şimdi topun hızını hesaplayın: 100metre/5saniye= 20metre/saniye. Muazzam! Siz de benim gibi aynı değeri buldunuz ve tenis topu fırlatma makinesi üreticisinin makinesinin kusursuz olduğu konusundaki iddialı söylemini (ışık hızı sabittir) doğruladınız. Tebrikler!

Bu örnekte zaman genişlemesinin, sadece kolunuzdaki saatle ilgili olmadığını, biyolojik saatiniz –ve trenin içindeki her şey- için de geçerli olduğunu anlıyoruz: Kalp atış hızınız yavaşlamakta, göz kırpma süreniz uzamakta, tenis topu makinenin namlusundan daha yavaş ayrılmakta kısaca trendeki her şey –düşünce hızınız bile- durgun haldeki zaman akışınıza göre ağır çekimde gerçekleşmektedir! Ancak siz vagonda sıra dışı hiç bir şey fark etmezdiniz, her şeyin normal bir hızla aktığını görürdünüz ama kendi saatinize göre normal! Sizi ve beni eş zamanlı ve karşılaştırmalı olarak izleyen üçüncü kişiler sizin benden iki kat daha yavaş hareket ettiğinizi görebilirdi. Bu konuda söylenecekler bitmez, o yüzden biz şimdi başka bir şeyler söyleyelim; kemerlerinizi sakın çözmeyin.

Zamanın mutlak olmadığını öğrendik. Tik-tak aralıkları uzayabiliyor, kısalabiliyor. Dolayısıyla zamanda hızlanabiliyor, yavaşlayabiliyoruz. Uzamsal boyutlarda da böyle olmuyor muydu? Hatırlayın, uzamsal boyutlar konusunu işlerken dünya çevresinde sabit bir hızla dönen uydunun hareketi uzamsal boyutlara farklı miktarlarda dağılabiliyordu. Şimdi zaman boyutunda da hareketimizin değişken olduğunu öğrendiğimize, zaman ve uzamsal boyutların aynı dokunun birleşik bir parçası olduğunu anlattığımıza ve evrenin hız limitinin ışık hızı olduğunu bildiğimize göre şunu söyleyemez miyiz?: uzay-zamanda her şey ışık hızında hareket etmektedir!

Kabul ediyoruz, sarsıcı bir ifade bu. Eğer söz konusu ışık ise, ışık zamanda hareketsizdir yani sonsuz ömürlüdür. Uzay-zamandaki bütün hareketini yani c sabit hızının tamamını uzayda yol alarak geçirir. Garajınızda hareketsiz duran otomobiliniz de ışık hızında hareket eder. Ancak ışıktan şöyle bir farkı vardır; bu hareketinin tamamı uzay-zamanın zaman boyutunda gerçekleşir yani zamanda ışık hızıyla yol alarak eskir arabanız. Peki otomobilinizi garajından çıkarıp sürmeye başlarsanız? Bu durumda aracın uzay-zamanın zaman boyutundaki hareketi yavaşlar ve bu yavaşlama oranında uzay boyutlarında hareket etmeye başlar, yani yol almaya başlar. Tahmin edeceğiniz gibi, otomobilin gazına ne kadar basarsanız uzay-zamanın zaman boyutundaki hareketi o kadar yavaşlar, uzaydaki (yol) hareketi o kadar artar. Ancak her iki boyutta gerçekleşen hareketin toplamı değişmez: “c”. Otomobilinizi ışık hızında kullanabilseydiniz zaman tamamen dururdu, aracınız hiç eskimezdi.

Özel görelilik kuramının bizi ilgilendiren diğer bir sonucu uzunluk büzülmesidir. Bu fenomene neden olan şey ise zamanın göreli hale gelmiş olmasıdır. Hatta sadece uzunluk değil zamana göre ifade edilebilen bütün fiziksel büyüklüklerin göreli hale geldiğini söyleyebiliriz. Burada kısaca ele alacağımız konu bu büyüklüklerden birisi olan uzunluktur. Hareketli bir cismin uzunluğu, durgun halde ölçülen uzunluğuna göre daha kısadır. Buna Lorentz-Fitzgerald daralması (uzunluk büzülmesi) diyoruz. Neden Einstein daralması değil? Çünkü ışık hızının sabit oluşundan kaynaklı olarak böyle bir etkinin oluşabileceği Einstein’den önce Hendrik Antoon Lorentz ve George Fitzgerald tarafından ayrı ayrı öngörülmüştü. Demek ki Einstein’in özel görelilik kuramı bilim tarihinde birdenbire gerçekleşen bir sıçrama değil, kendisinden önceki çalışmalara dayanan daha kapsayıcı ve tamamlayıcı bir bakış açısıdır. Aynı şey genel görelilik kuramı içinde geçerlidir; yeri geldiğinde söyleyeceğiz bunu. Şimdi uzunluk büzülmesine dönelim tekrar.

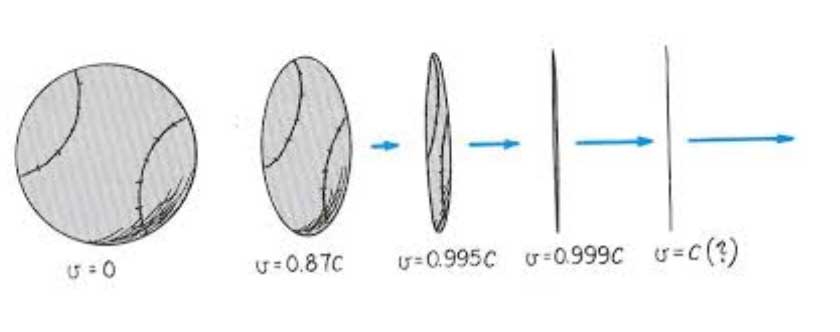
Bir cismin durgun ve hareketli iken uzunlukları aynı değildir. Hareket etmekte olan bir cismin uzunluğu cisme dışarıdan bakan bir gözlemci için hareket ettiği yönde kısa görünür, kısa ölçülür. (Cismin yüksekliği Lorentz-Fitzgerald daralmasına uğramaz çünkü cismin yüksekliği hareket yönüne diktir yani yükseklik eksenindeki hareketi sıfırdır) Peki cismin içindeki gözlemci bunu fark etmez mi? Hayır etmez. Örneğin kullanacağı terzi metresi de cisimle aynı oranda uzunluk büzülmesine uğrayacağından –kendisi bunu fark edemez- dışarıdaki gözlemci ile aynı uzunluğu bulacaktır. Peki gerçekten de cismin boyu hareket doğrultusunda kısalıyor mu yoksa bu sadece fiziğin durumu kılıfına uydurmasından mı ibaret? Cevap birincisi. Zamanın genişlemesi ve her şeyin ışık hızında hareket ettiğini öğrenmiş olmak her ne kadar şaşırma eşiğinizi yükseltmiş olsa da bu durum size yine de şaşırtıcı gelmiş olmalıdır. Şimdi kemerlerinizi çözebilirsiniz. :)

Artık elimizde Newton ve Gallilei’nin mutlak uzay ve mutlak zamanı yerine oyun hamuru gibi şekilden şekle girebilen bir uzay-zaman dokusu var. Onu istediğiniz şekle sokabilirsiniz. Ama bunun için biraz geometri hakkında konuşmamız gerekiyor.

4. Bölüm: Öklid Dışı Geometriler

Yunan matematikçi Öklid (Eukleides) doğruluğundan şüphelenilmeyen bir takım temel önermeler (aksiyom) ışığında bazı postülalar öne sürmüş ve bu postülalardan hareketle de kendi adıyla bilinen Öklid geometrisini inşa etmiştir. Bu postülatlar şunlardır:1- İki yol arasını birleştiren en kısa yol, doğrudur2- Doğru olarak sonsuza kadar uzatılabilir.3- Bir noktaya eşit uzaklıkta bulunan noktaların geometrik yeri çemberdir.4- Bütün dik açılar birbirine eşittir.5- İki doğru bir üçüncü doğru tarafından kesilirse, içte meydana gelen açıların toplamının 180^o`den küçük olduğu tarafta bu iki doğru kesişir.6- Bir üçgenin iç açıları toplamı 180<sup>o</sup>`dir.7- Bir doğruya dışındaki bir noktadan yalnızca bir tek paralel çizilebilir.Ancak bu ifadelerin kesinliği 19.yy’da matematikçiler tarafından ciddi şekilde sorgulanmış ve özellikle Bernhard Riemann ile Nikolay Lobachevsky’in yaptıkları önemli çalışmalarla öklid-dışı geometriler ortaya çıkmıştır. Örneğin bir Öklid uzayında çizilen üçgenin iç açılarının toplamı 180^o olmak zorundadır. Ancak pozitif eğriliğe sahip yani küresel bir uzayda üçgenin iç açılarının toplamı 180^o’den büyük iken, negatif eğriliğe sahip yani eyer biçiminde olan bir uzayda 180^o’den küçüktür.

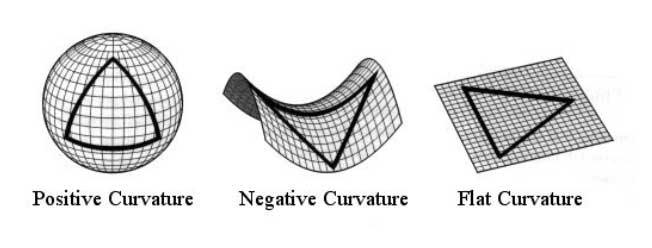
Öklid geometrisinin bir başka defosu bir noktaya dışındaki bir noktadan yalnızca bir tek paralel çizilebileceğini iddia etmesinden doğar. Halbuki pozitif eğimli bir uzayda paraleller eninde sonunda birbiriyle kesişir. Negatif eğimli uzayda ise paraleller Öklid geometrisinde olduğu gibi kesişmezler ancak daha başka tuhaf bir durum ortaya çıkar; bir doğruya dışındaki bir noktadan sonsuz sayıda paralel çekilebilmektedir!

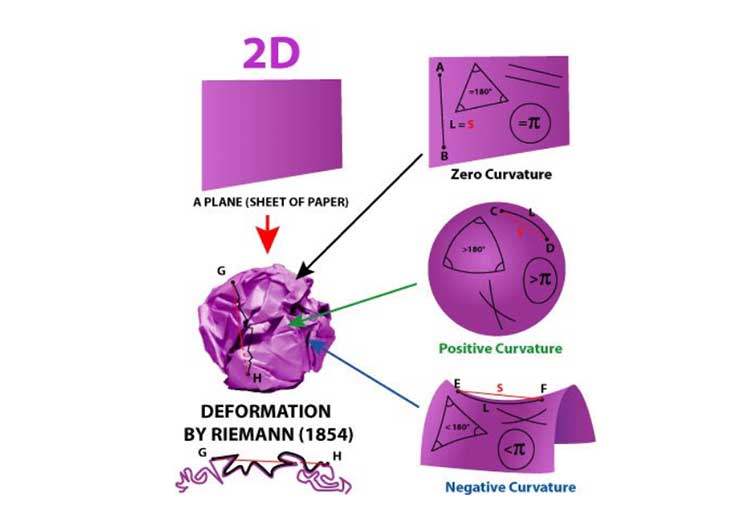
Yukarıdaki şekilleri inceleyin. Sıfır eğimli bir uzaya (zero curvature) çizdiğiniz çemberin çevresinin çapına oranının (pi) sayısını verdiğini hepiniz biliyorsunuzdur. Bu geometrinin değişmez bir yasasıdır değil mi? Peki bu çember pozitif eğimli bir uzaya çizilirse çevrenin çapa oranı yine pi sayısını verir mi? Cevap hayır! Böyle bir uzaya çizilmiş çemberin çevresinin çapına oranı pi sayısından büyük bir değer alır! Negatif eğri uzaydaki çemberin çevresinin çapına oranı ise pi sayısından küçük çıkacaktır! Demek ki geometride değişmez bir yasa yokmuş. Şimdi daha önce oyun hamuru haline getirdiğimiz uzay-zamanı zihnimizde şekilden şekle sokacak geometri bilgisine sahibiz. Artık genel göreliliği inşa edebiliriz! Hadi başlayalım o zaman, ne duruyoruz?

5. Bölüm: Genel görelilik kuramının inşası ve sonuçları

Alaaddin'in sihirli lambasindaki cin, lambadan çıkarılması karşılığında kendisinden dilenen çok kötü niyetli bir dileği yerine getirmiş olup güneşi yok etmiş olsaydı, Newton’un evrensel çekim yasasına göre bu dilek gerçekleştiği anda dünya kararır, ve güneşin kütleçekim kuvveti “anında” yok olduğu için uzaya savrulurdu. Ancak bu senaryoda çok ciddi bir sıkıntı vardır. Özel görelilik kuramına göre hiçbir bilgi, hiçbir kuvvet, ışıktan hızlı hareket edemez. Dolayısıyla güneşin yok olmasının etkilerini ancak 8 dakika kadar bir zaman geçtikten sonra hissetmemiz gerekir. O halde kütleçekim konusuna devrimci bir bakış açısı getirmemiz gerektiği ortadadır. İşte Albert Einstein 1915 yılında bu devrimi gerçekleştirdi. Size özel görelilik kuramının kendi başına bir sıçrama olmadığını, belli bir teorik ve matematiksel altyapı üzerinde inşa edilmiş şık ve derli toplu bir kuram olduğunu söylemiştik. Genel görelilik kuramı da böyledir. Einstein genel görelilik kuramını kuramdan önce oluşturulmuş olan geometrik çerçeveye oturttu. Bu çerçeve olmasaydı belki de Einstein’in o zengin hayalgücü bilimsel bir niteliğe bürünemeyecekti. Şimdi ilk dört bölümde öğrendiklerimizi uygulamaya geçirelim ve ikinci görelilik devriminin nasıl gerçekleştiğini anlamaya çalışalım.

Bir bisiklet jantının tam göbeğinde bir karınca olsun. Jant sabit bir hızla dönmektedir. Karınca göbekten jant çerçevesine doğru mil üzerinde sabit bir hızla yürümeye başlasın.Karıncanın mil boyunca yaptığı bu yolculukta hareketi hakkında ne söyleyebiliriz? Mil boyunca sabit bir hızla yürüdüğünü söyledik, yani doğrusal olarak hızı değişmez. Peki dönme hızı için ne söyleyebiliriz? Karınca göbekten çerçeveye yaklaştıkça dönme hızı artmaktadır. Yani çizgisel hızı artmaktadır. Açısal hızı ise değişmez çünkü jant da sabit hızla dönmekteydi. Şimdi anladığımız kadarıyla karınca çerçeveye yaklaştıkça karıncanın dönme hızı sürekli olarak artmaktadır. Çerçeveye ulaştığında ise dönme hızı maksimuma ulaşmıştır. O halde karıncanın mil üzerindeki yürüyüşü boyunca dönme hızı düzgün ve sürekli bir şekilde arttığına göre karınca ivmeli hareket yapmıştır diyebiliriz.

Peki karıncanın dönme hızı sürekli arttığına göre karıncanın kolundaki saat bu yolculuktan nasıl etkilenir? Tahmin ettiğinizi biliyorum; özel görelilik kuramında öğrendiğimize göre karıncanın dönme hızı arttıkça kolundaki saatin yavaşlaması gerekmektedir. Bunu bir görselle destekleyelim:

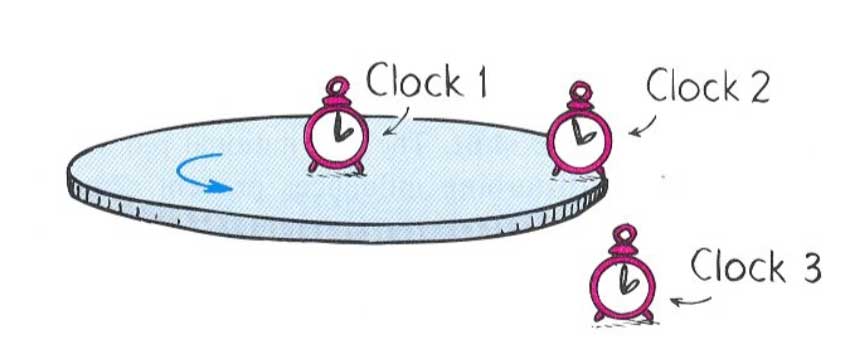
Clock-3, referans saatidir. Karınca göbekten harekete başladığı anda saat Clock-1`i gösteriyor yani referans saat ile senkronizedir, aynıdır. Karınca çerçeveye vardığı anda kolundaki saat Clock-2’i gösteriyor. Yani Clock-3’ün gerisinde kalmış. Demek ki burada zaman genişlemesi meydana gelmiştir.

Peki jantın fiziksel yapısı hakkında ne söyleyebiliriz? Mesela jantın yarıçap veya çevre uzunluğu değişir mi?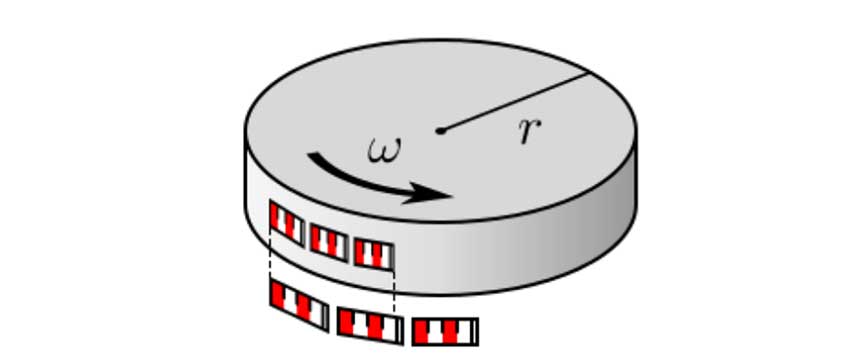

Evet, değişir: Jantın yarıçap uzunluğu değişmezken, çerçeve uzunluğu kısalır. Yani jant çerçevesi Lorentz-Fitzgerald daralmasına, yani uzunluk büzülmesine uğrar. Hatırlarsanız bu etki hareket doğrultusu boyunca cismin uzunluğunun kısalmasına neden oluyordu. Yarıçap (r) yani mil eksenleri hareket doğrultusuna diktir, yani uzunluk büzülmesine uğramaz ve aynı kalır. Çerçeve ise dairesel hareketin doğrultusu üzerinde w hızıyla dönmektedir ve dolayısıyla uzunluk büzülmesine uğrar. Bu kısım aklımızda tutmamız gereken üçüncü önemli noktaydı. (Görselde dairenin dışındaki üç uzunluk parçası, jantın durgun haldeki çerçeve uzunluğunu temsil ediyor. Jant dönmeye başladığında parçaların kısaldıklarına dikkat edin)

Şimdi eldeki verileri toparlayalım ve sonuca gidelim. Jant hareketli iken yarıçapı değişmediği halde çerçeve uzunluğu kısaldı. Bir öklid uzayında jantın çerçeve uzunluğunun kısalması yarıçapının da kısalmasını gerektirirdi.Peki yarıçapı değiştirmeden daha kısa çerçeve uzunluğuna sahip bir çember nasıl bir uzayda ifade edilebilir? Cevap; negatif eğriliğe sahip uzayda yani bir eyer üzerinde! Demek ki “ivmeli hareketin fiziksel ifadesi (zaman genişlemesi ve uzunluk büzülmesi) eğri uzay ilişkileri gerektirir” Yani zaman boyutu genişleyebilen, uzamsal boyutları kısalabilen oyun hamuru gibi esnek bir uzay-zaman dokusu!Şimdi kemerlerinizi bağlayın, biraz önce yazdığımız koyu puntolu cümleden “ivmeli hareket” cümlesini çıkarıp yerine “kütleçekim kuvveti” yazacağız. Bunu neden yapmayalım? Eşdeğerlik ilkesi bize bu yetkiyi fazlasıyla vermiyor mu?

“Kütleçekim kuvvetinin fiziksel ifadesi eğri uzay ilişkileri gerektirir."

Genel görelilik teorisi doğmuştur. Bu ifadeye göre kütlesi olan her şey, uzay-zamanı büker. Bir kütle tarafından bükülmüş uzay-zaman dokusunda hareket eden bir başka cisim bu eğri dokuyu takip eder. Yani aslında iki kütlenin birbirini çektiği yoktur; hareketi yöneten uzay-zamanın eğriliğidir!

Einstein gelmiş geçmiş belki de en büyük kuramsal fizikçidir diyebiliriz. Ancak bilim zekanız veya hayal gücünüzle değil, deney ve gözlem sonuçlarıyla ilgilenir. Eğer kütle Einstein'in dediği gibi uzay-zamanı gerçekten büküyorsa, bunun bir alametinin olması gerekir. O alamet yakınlarda bir yerdeydi. Evet, o güneşti. Güneş muazzam kütlesiyle uzay-zamanı büküyor olmalıydı. Hatta Einstein bu bükülme açısını bile teorik olarak hesaplamıştı. Buna göre güneşin yüzeyini tabiri caizse "yalayıp geçen" bir yıldızın ışığının 1,75 ark-saniyelik bir açıyla sapması gerekiyordu.

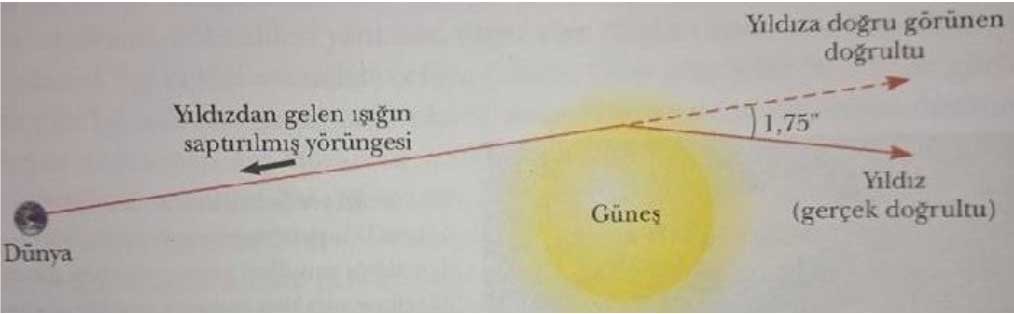
Çünkü ışık uzay-zamanı takip ettiğine ve uzay-zaman bükülmüş olduğuna göre ışığın doğrultusundaki değişim bize kuramın deneysel ispatını sunacaktı. Gerçek konumu A olan bir yıldızdan gelen ışınlar güneş tarafından bükülen uzay-zamanı kat edip dünyaya ulaşır ve onu B noktasındaymış gibi görürüz.

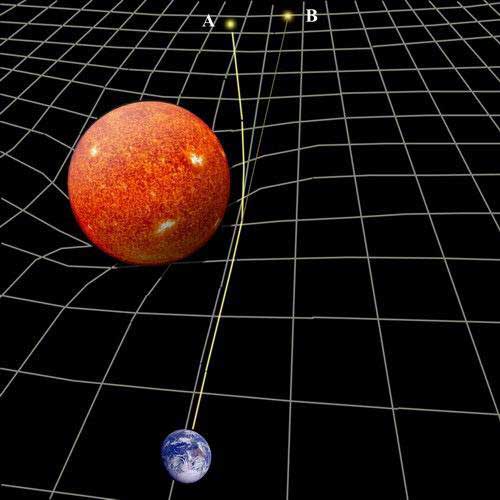İyi de, gündüz vakti nasıl gözlem yapacağız? Güneş, yıldızdan gelen ışığı bastırmaz mı? Gece yapalım desek bu kez de gökyüzünde güneş olmadığından ışığın bükülme açısını hesaplayamayız? Bilimsel bir kuram sınanmak üzere hazır bekliyorsa, onu sınayacak deneyin kurgulanması pek uzun sürmez: gözlem güneş tutulması esnasında yapılacaktı. Tutulma esnasında gökyüzü kararır ve yıldızlar belirir. Tutulmuş güneşe çok yakın görünen bir yıldıza ait ışınlar, uzay-zamanın eğriliğinden etkilenmiş olmalıdır. Bu yıldızın görünen konumunun (B) tutulma esnasında uzak bir referans yıldızıyla yaptığı açı ölçülür. Ardından tutulma yokken açı ölçümü yapılır. Tutulma yokken yıldız gökyüzünde gerçek konumuyla (A) gözleneceği için referans yıldızla yaptığı açı değişecektir. Gerçekten de böyle bir fark varsa, bu, ışığın bükülmüş bir uzay-zaman dokusunda yol almış olduğunun yani genel görelilik kuramının ispatı olacaktı. Batı

Kuramın ortaya atılmasının üzerinden 3 yıl geçmişti. İngiliz astronom Arthur Eddington 29 Mayıs 1919’da Batı Afrika’da Principe adasında güneş tutulmasını gözlemledi ve bolca fotoğraf çekti. Yaptığı detaylı incelemeler sonucunda yıldızlardan gelen ışığının saptığını ortaya koydu. Kuram doğrulanmıştı.

Genel görelilik kuramı sadece ışığın sapma açısını öngörmemiştir. Örneğin uzay-zamanda çok şiddetli bazı kozmik olaylar neticesinde oluşan kütleçekim dalgaları olmalıydı. Bu öngörü de çok yakın bir zamanda, 2015 yılında Lazer İnterferometre kütleçekimsel dalga gözlemevi (LIGO) tarafından doğrulanmıştı. Ayrıca kütleçekimsel mercekleme etkisi ve kara delikler genel görelilik kuramıyla açıklanabilen kozmik cisimlerdir.

Sonuç olarak genel görelilik kuramı bir kütleçekim teorisi olarak astronomik ölçekte kütleçekim olgusunu başarıyla açıklamaktadır. Ancak daha küçük ölçeklerde (kuantum seviyeleri) kütleçekimin mekanizmasına aydınlatacak nihai bir kuram da değildir. Genel göreliliği kuantum mekaniği ile birlikte yorumlayarak nihai bir kütleçekim kuramının oluşturulması yönünde yoğun çabalar devam etmektedir.

Yolculuğumuz buraya kadardı. Şimdi sözü o’na bırakabiliriz:

Mantık sizi A noktasından B noktasına götürür, hayalgücü ise her yere... Albert Einstein (1879-1955)