Uzay Bir Etkileşim Haritası Olabilir mi?
Zamanın varolmadığını, yani evrenin bir zaman boyutuna sahip olmadığını düşünen İngiliz fizikçi Julian Barbour, uzayın doğal dünyanın düzenleyici ilkesi olarak görev yaptığını söylemişti; tıpkı evreni bir arada tutan bir yapıştırıcı gibi. Fiziksel nesneler kendi isteklerine göre değil, belli bir anda uzayda bulundukları konumlara bağlı olan aralarındaki ilişki tarafından belirlenen davranışlar sergiliyorlardı. Bu yapılandırma rolü, mekanik hareketin klasik yasalarında kolayca görülür. Aynı zamanda alan kuramlarında da mevcuttur. Bir alanın farklı uzay noktalarındaki değeri ve değişim hızı, alanın ne yaptığını bütünüyle belirler ve alan noktaları sadece kapı komşuları ile etkileşir.
Bu tür davranışlar "yerellik"i (İng. locality) ifade eder; her şeyin bir yeri vardır. Bir nesneye her zaman işaret edebilir ve "işte orada" diyebilirsiniz. Deneyimlediğimiz dünya yerelliğin tüm niteliklerini taşır. Güçlü bir "yer ve yerler arası ilişki" anlayışına sahibizdir. Yerellik, benlik bilincimizin de temelini oluşturur; kendi duygu ve düşüncelerimizin kendimize ait olduğuna güveniriz. Her insan, diğerlerinden uzay denizi ile ayrılmış birer adacık gibidir.
Ancak yerellik artık eskiden olduğu şey değil. Kuantum mekaniği, iki parçacığın dolaşık olabileceğini öngörüyor. Dolaşık parçacıklar, aralarındaki uzaklık ne olursa olsun, birbirlerinin durumlarından etkilenebiliyorlar. Görünüşe bakılırsa evrenimiz, bu gizemli ilişkilerden örülmüş bir ağ. Evet, geçtiğimiz 20 yıl içinde, fizikçilerin yerelliğe bakışlarının nasıl değiştiğine tanık olduk ve "Gözümle görmesem inanmazdım ama anlaşılan evren yerel değil," diyen fizikçiler duyduk.
Düzeni Sağlıyor mu, Tanımlıyor mu?
Yerel olmayışın (İng. nonlocality) ne olduğunu anlamak için ilk önce uzay anlayışımızı ters-yüz etmemiz gerekiyor. Fizikçiler ve felsefeciler uzayı, doğal dünyanın belli bir şekilde yapılandığı bir olgu olarak betimleyebilirler. Uzayın evrene düzen sağladığını söylemek yerine, evrenin düzene sahip olduğu ve uzayın da bu düzeni tanımlamaya elverişli bir kavram olduğu söylenebilir.
Nesnelerin birbirlerini belli biçimlerde etkilediklerini algılarız ve bu sayede onlara uzayda konumlar atfederiz. Bu yapının iki önemli yönü vardır. Birincisi, etkiler hiyerarşiktir. Bazı şeyler bizi, başka bazı şeylerden daha fazla etkiler ve bu fark sayesinde uzaklıklarını çıkarsayabiliriz. Zayıf bir etki uzaklık anlamına gelir; güçlü bir etki ise yakınlık. Felsefeci David Albert, uzaklığın bu tanımını "interaktif uzaklık" olarak adlandırıyor. Yani bu anlayış uyarınca "Aslan çok yakın, üstümüze atlayabilir," demek yerine, "Aslan üstümüze atlayabilir, demek ki çok yakın," demeniz uygun düşüyor.

Uzaysal yapının ikinci yönü ise çok çeşitli etkilerin karşılıklı olarak uyumlu oluşlarıdır. Eğer bir gergedan da üstüme atlayabilecek durumdaysa, o da çok yakında demektir. Ayrıca eğer hem bir aslan hem de bir gergedan üstüme atlayabilecek durumdaysalar, o zaman aslan ile gergedan birbirlerinin de üstüne atlayabilecek durumdalar demektir.
Etkilerin bu şablonundan, uzayı elde ederiz. Eğer yukarıda sözünü ettiğimiz hayvanların oluşturduğu tehdit, uzaysal uzaklık cinsinden ifade edilemeseydi, uzay anlamsızlaşırdı. Hayati tehlikesi daha az olan bir örnek vermek gerekirse "üçgenleme"yi (nirengi) düşünebiliriz. Cep telefonunuzun bağlantı sinyal çizgileri, baz istasyonuna olan uzaklığınızı belirtir. Acil bir durumda, servis sağlayıcınız sinyalinizin çeşitli istasyonlardaki durumunu ölçüp, üçgenleme ile konumunuzu saptayabilir. Ölçümlerin tek bir noktaya yakınsaması, sizin için bir konumda bulunmak anlamına gelir.
Evrenin Olası Durumlarından Biri
Uzayı "yapı olarak" betimlemenin güzel yanı, uzayın doğasına ilişkin epeydir süren uyuşmazlıklardan kaçınmayı sağlaması. Antik atomcular (Newton dahil), uzayı kendi başına varolan bir şey olarak düşünürdü. Öte yandan Aristo (Leibniz ve Mach gibi) uzayı, evrende varolan şeylerin nasıl bir arada olduğunu tanımlayan bir soyutlama olarak algılardı. Bu bakış açılarının ikisinde de uzay, evrenin sahip olduğu bir yapıyı yansıtmaktaydı. Eğer atomcular haklı olup uzayın kendi bağımsız varlığı olsaydı, titizlikle dikilmiş bir kumaş gibi yüksek düzenliliğe sahip olurdu ve böylece fiziğin ondan talep ettiği işlevleri yerine getirirdi. Uzay sadece bir soyutlamadan ibaret olsaydı da evrenin içindekiler soyutlamaya anlam kazandıracak doğru biçimde uyuşurlardı.
Görünüşe göre, düzenlemeye öncelik vermek bize bir şey kazandırmıyor; sadece bir gizem yerine başkasını ediniyoruz. Çünkü bu kez de düzenlemeyi açıklamamız gerekiyor. Fakat bu bir fırsat olabilir, çünkü o vakit evren eğer gereken şekilde düzenlemese neye benzeyeceğini hayal edebiliriz. O durumda uzaysal olmazdı. Uzayı mutlak gereklilik olarak düşünmek yerine, evrenin olası durumlarından biri olarak alabiliriz; tıpkı buzun olası su hâllerinden biri olması gibi. Aslında buz benzetmesi hiç de fena değil. Suyun katı olabildiği koşullar, gaz olabildiklerinden çok daha sınırlıdır. Benzer şekilde, uzay bir kural değil de, istisna olabilir. Öne sürülen birleşik fizik kuramlarının çoğu, evrenin olası durumlarının çok büyük bölümünün uzaysal olmadığını ileri sürüyor. British Columbia Üniversitesi'nden sicim kuramcısı Moshe Rozali, uzay-zamanın varolduğu durumların hiç de genel olmadığını, bazı özel koşullar gerektirdiğini belirtiyor. Düzen ile düzensizlik, uzay ile uzaysızlık arası alacakaranlıkta, belki de fizikçilerin kafasını kurcalayan yerel olmayış görüngüleri için kavranabilir bir açıklama bulabiliriz.
Konumun Anlamsızlaştığı Bir Evren
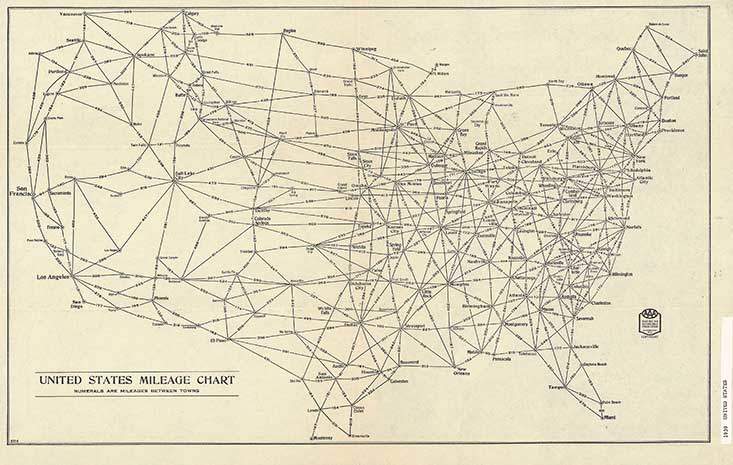
Uzayın düzenleyici gücünün farkına varmak için hareket eden ve etkileşen parçacıkların karmaşık bir sistemi gerekli değil. Bir ülkenin coğrafyasını düşünün. Şehirleri bir haritanın üzerine yayılmış şekilleriyle veya karşılıklı uzaysal ilişkilerinin ifade edildiği bir kilometre tablosu ile düşünebilirsiniz. Kilometre tabloları genellikle yol haritalarına eklenir; şehir çiftleri arasındaki uzaklıkların okunabildiği üçgen veya dikdörtgen şekilli ızgaralara benzerler. İşin ilginci, kilometre tablolarında gizli şablonlar vardır.
Örneğin 20 tane şehrimiz olsun. Kilometre tablosunda 400 tane sayı olur. Verileri doldurmak için harita şirketi sürücüleri görevlendirir ve onlardan şehirden şehire giderken kilometre göstergesindeki değişimi not etmelerini ister. Gerçek veri içeriği bakımından, dikdörtgen bir tablo oldukça hantaldır. Uzaklıklar, matematikçiler tarafından "uzaklık aksiyomları" olarak adlandırılan belli kurallara uyarlar. Dikdörtgen tablolarda köşegen boyunca uzanan 20 sayı sıfır olur: Her şehrin kendine olan uzaklığı sıfırdır. Köşegenin iki yanı da simetriktir: A şehrinden B şehrine gidiş yolu ile B şehrinden A şehrine gidiş yolunun aynı olduğu kabul edilir. Dolayısıyla çoğu harita firması, kilometre tablolarını sadece üçgen şeklinde sunar.
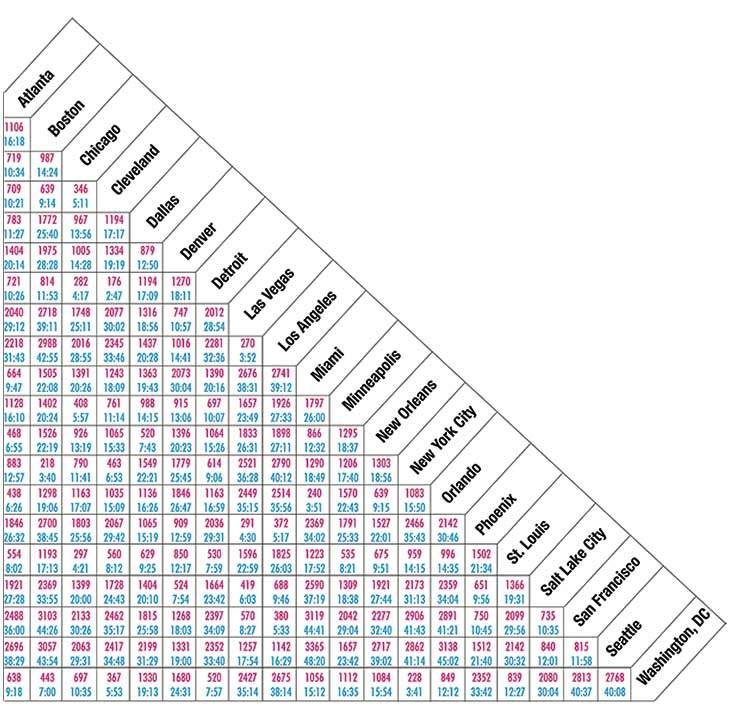
Liste daha da indirgenerek, sadece 55 sayı ile ifade edilebilir.
Bu tür sıkıştırma, uzaysal düzenlemenin karakteristiğidir. Görsel Telif: AAA
Aslında bu üçgendeki 190 nicelik bile birbirinden bütünüyle bağımsız değildir; çünkü onlar da herbir şehrin koordinatlarını temsil eden 60 değere indirgenebilir: Enlem, boylam ve irtifa. Gezegenin eğiminin önem kazandığı kadar birbirinden uzak olan şehirler için Dünya'nın yarıçap verisini de eklemek gerekebilir. Son olarak, koordinat sistemi üzerinde yapılan anlaşmalar (birinci meridyenin sıfırıncı boylam olması gibi), sürüş açısından bir anlam ifade etmediğinden birkaç rakamdan daha kurtulabiliriz. Böylece 6 nicelik daha gider ve kalır geriye 55 rakam. Tabloya bir bakışta bunlar fark edilmeyebilir, ama tersinden giderek bunun sağlamasını yapabilirsiniz. Şehirlerin koordinatları ile başlayıp, haritada konumlarını işaretleyip, şehirlerarası uzaklıkları bulmak için trigonometriden yararlanabilirsiniz.
Yani bu tablo yüksek bir düzene sahiptir. Şehirlerin uzayda yer almasının anlamı budur. Uzaysal koordinatlar, nesneler arasındaki olası karşılıklı ilişkileri yakalamanın çok ekonomik bir yoludur. Yukarıdaki örnekte 20 şehrimiz vardı ve biz 400 tane uzaklığı 55 rakama indirgeyebildik. Ne kadar fazla şey varsa, indirgeme o kadar etkileyici olur. 100 şehir için 10.000 tane uzaklık veren bir tablo, 295 rakama indirgenebilir. Tek bir dünya haritasında, gezegendeki tüm şehirleri coğrafik özellikleri ile gösterebilirken, bunu mesafe tablosu şeklinde indirgemeden saklamak için epeyce hard disk alanı gerekir. "İşte uzay bu," diyor Barbour. "Devasa ölçekte veri sıkıştırma yapıyor."
Sıkıştırmanın bu denli güçlü olmasının nedeni yerellik. Yerelliğin anlamı şudur: Bütün, uzaysal parçalarının toplamıdır ve bu bağlamda her yolculuk, bir dizi küçük adım anlamına gelir. Uzun mesafeleri, daha kısa ara adımlardan yapılandırabilirsiniz. Dolayısıyla herbir rota çiftini teker teker belirtmenize gerek kalmaz. Örneğin, tablo size Dallas'tan Denver'a 900 mil ve Denver'dan Salt Lake City'e 500 mil olduğunu söylediğinde, Dallas'tan Salt Lake'e 1.400 mil olduğunu belirtmesine gerek kalmaz.
Şimdi de durumun böyle olmadığını varsayalım; diyelim ki tablodaki veri böyle yüksek düzeyde düzenli olmasın. Eğer tabloyu rastgele 400 sayı ile doldursam ve sizden bunların konumlarını haritada işaretlemenizi istesem, başarmanız pek mümkün olmaz. Örnek vermek gerekirse, tablo size Dallas'tan Denver'a 900 mil, Denver'dan Salt Lake City'e 500 mil ve Dallas'tan Salt Lake City'e 8.000 olduğunu söylesin. Bu pek akla yatmıyor, değil mi? Veriler, Dallas'tan doğrudan gitmeye ya da Denver'dan geçerek gitmeye bağlı olarak, Salt Lake City'i iki ayrı konuma koyuyor. Yapbozun parçaları birbirine uyuşmuyor.
Böyle durumlarda konum anlamsızlaşır. Uzay anlamsız hâle gelir. Konumlar arası ilişkileri betimlemenin kullanışlı bir yolu olmaktan çıkar. Ama bu, şehirlerin göreli düzenlenişlerinin kavranılamaz olduğu demek değildir. Şehirleri haritada işaretleyemeseniz bile, toplu mesafe tablosuna geri dönebilirsiniz. Bir başka deyişle, felsefecilerin verdiği adla "aracısız/ dolayımsız/ doğrudan" (İng. unmediated) uzaklıkları kullanabilirsiniz; bunlar doğrudan şehir çiftlerini ilişkilendirirler ve daha kısa sıçramlara indirgenemezler. Tabi bu bütünüyle varsayımsal bir durum. Boston'da araba kullanırken, uzaysal farkındalığınıza güvenmeseniz iyi olur, çünkü kaybolursunuz. Bu amip şekilli "göbek"ler ve tek yönlü caddeler labirentinde, çoğu zaman batıya gitmek için doğuya dönmeniz, sağa dönmek için sol şerite geçmeniz gerekir. Kuş bakışı nerenin nerede olduğunu bilmenin yararı yoktur; ne zaman nereye sapacağınıza ilişkin yönergeleri robot gibi izlemek zorundasınız. Yani bir sürücü için Boston "uzaysal olmayan" (İng. nonspatial) bir şehirdir.
New York'tan Boston'a en kısa mesafenin, Boston'dan New York'a en kısa mesafe ile aynı olması gibi.
Görsel Telif: AAA
Sosyal Uzay
İlişkiler ağının uzayın dışına taşması ise o kadar da garip karşılanmaz. İnsanlar arası ilişkilerdeki durum sonuçta budur. Sosyal yaşamımız, uzaysal bir haritaya yansıtılamayacak kadar karışıktır. İnsanlar denemiyor değil. Örneğin soy ağaçları, genetik ve evlilik ilişkilerini, uzaysal ilişkiler biçimine dönüştürür. Internetteki sosyal ağlar da bunun benzerini denemiştir. Mesela The Wolfram Alpha sitesinde, Facebook arkadaşlarınız arası ilişkileri, kişileri simgeleyen noktaları birleştiren çizgiler şeklimde haritalayabiliyordunuz.1 Noktalar arası uzaklık, yani çizgilerin uzunluğu, kişilerin muhattabiyet derecesi ve ortak arkadaş sayısı ile belirleniyordu. Tipik olarak insanlar ayrık sosyal çemberler şeklinde kümeleniyorlardı: Aile, okul arkadaşları, iş arkadaşları, falanca takımın taraftarları ve filanca şarkıcının dinleyicileri gibi. Bu insanların hepsini partiye davet etseniz, muhtemelen tıpkı o haritadaki noktacıklar gibi gruplaşırlardı.
Bu Facebook haritalarının en eğlenceli yanı, bazen hiç beklemediğiniz bağlantıları ortaya sermesiydi. Örneğin bir iş arkadaşınızın, müzik zevkinize bağlı olarak tanışık olduğunuz kişilerle tanışıklığını fark edip, benzer müzik dinlediğinizi fark edebiliyordunuz. Bu durum aynı zamanda uzaysal metaforun sınırlamalarını da gösteriyordu. İş arkadaşınızı grafiğe yerleştirebileceğiniz tutarlı bir yer olmuyordu. Yukarıdaki Salt Lake City örneği gibi, iki farklı sosyal çembere karşılık gelen iki ayrı konum işgal ediyordu. Ayrıca bu grafikler, bazen yüz yüze hiç görüşmemiş insanları birbirlerinin en yakın arkadaşıymış gibi gösterebiliyordu. İnsan ilişkilerinin diğer boyutlarını gösterebilmek için bazen soy ağaçlarında farklı çizgi biçimleri kullanılırdı: Yakın ilişki için kalın çizgi, hoşlaşmama için zikzak gibi. Uzaysal metaforun yetersizliği böylece biraz olsun azalırdı.
Bazen de insanlar kendilerini öyle bir şekide düzenlerler ki, sosyal ağ alışılmadık ölçüde düzene girer. Daha önce varolmayan bir yapı belirir. Bu iki şekilde olabilir: Oluşturarak veya budayarak. İlkine örnek olarak, sonunda bir Facebook hesabı açmaya karar verip, gerçekten tanıyıp bildiği kişileri ekleyen anneannenizi verebiliriz. İkincisine örnek olarak ise girdiği her ortamda, her insanla kaynaşan ve Facebook'ta da her önüne geleni listesine ekleyen birinin, sonunda bu insanların yarısından fazlasını tanımadığını fark edip silmesi verilebilir.
Örneğin orduda sosyalleşme rütbelerle kısıtlanır. Farklı rütbeler, uzaysal mesafelere benzer. Bir erin subaya olan uzaklığı, Salt Lake City'nin Dallas'a uzaklığı gibidir: Er ile subay arası bilgi akışı, iki şehir arasındaki orta noktalardan geçen sürücü gibi bir yol ile gerçekleşir.Bu yapıdan ötürü, askeri hiyerarşi tablosu, ordudaki sosyal ilişkileri oldukça iyi betimler.
Ordunun yapısı askeri disipline bağlı olarak oluşur. Başka durumlarda ise düzen kendiliğinden belirir. Klasik bir örnek pazar ekonomisidir. Sanki ellerindeki parayla ilgili kararlar veren milyonlarca insan değil de, bilinçli bir canlıymış gibi "ekonomi"den söz ederiz. Aslında bir açıdan da öyledir, çünkü toplu düzenleme onu yaratan insanları aşar. Bireyler tek başlarına bir şeylerin üzerine fiyat etiketi yapıştırmaz; çünkü satacak ya da alacak kimse yoktur. İnsanlar bir araya gelip değiş-tokuşa başladığında fiyat anlam kazanır. Ücretler kişiden kişiye ve yerden yere değişir. Bu değişkelerden yararlanan bazı girişimciler, ucuza alıp pahalıya satmayı başarır.

Görsel Telif: Wolfram Alpha LLC, 2014
Bu tür bir öz-düzenleme fizikte her zaman olur. Örneğin tek bir su molekülünün sıcaklığından söz edilemez. Sıcaklık, moleküller bir araya gelip çarpışmaya ve enerji alışverişine başladıklarında anlam kazanır. Sıcak ve soğuk suları karıştırırsanız, denge sağlanana dek sıcak olan soğur ve soğuk olan ısınır. Dengeden önce iki sıcaklık değeri ile karakteriz edilen su, tek değere indirgenir. Karmaşıklıktan basitliğe gidilir. Yine de karmaşıklık, örtülü olarak varlığını sürdürür. Ne zaman sıcaklıkta çalkantı olsa veya su hâl değişimine girse, orada belirir.
Aynı şey uzay için de geçerli olabilir. Doğanın temel yapıtaşları, karmaşık ilişkiler ağına sahip olabilir. Bazı düzenleyici mekanizmalar veya basitçe ortalamaların oyunu ile bu ilişkiler disipline edilebilir. Böylece uzaysal bir ızgaraya aktarıldıklarında, sadece belirli şekillerde etkileşebilirler. Kafa karıştırıcı karmaşıklıkta bir etkileşimler ağı, "konum" ve "zaman" adlarını verdiğimiz birkaç sayıya indirgenmiş olur. Yine de temelde yatan karmaşıklık yok olmamıştır. Kara delikler gibi bazı durumlarda, sistem düzensizleşebilir ve olaylar, konuma ya da zamana sahip olmayı kesebilir. Sistem uzaysalken bile, emgin miktarda örtük karmaşıklık içerir. Belki de uzaya yayılmış biçimde gördüğümüz evren, sadece yüzey katmanıdır; biz yüzeyde küçük sandallarla süzülürken, suyun altında kim bilir neler olmaktadır.- Nautilus, “Let’s Rethink Space“ (Kaynaktan özetlenen bu yazı, George Musser’ın “Uzaktan Hayaletimsi Etki” adlı kitabından derlenmiştir.) http://nautil.us/issue/32/space/lets-rethink-space
Dilediğiniz miktarda aylık veya tek seferlik bağış yapabilirsiniz.
Destek OlBunlar da İlginizi Çekebilir