Mach İlkesi Nedir?
Yazımıza başlamadan önce fizik literatürüne bir bakalım bu ilkenin tanımı noktasında. Hali hazırda literatüründe Mach ilkesinin ondan fazla yorumu bulunmakta.
Yazımıza başlamadan önce fizik literatürüne bir bakalım bu ilkenin tanımı noktasında. Hali hazırda literatüründe Mach ilkesinin ondan fazla yorumu bulunmakta. Bunlardan bazıları teknik olsa da (fizikçi olmayan okurlar için burada önemli olan her birinin teknik detayları değil, literatürde bu ilke üzerinde bir uzlaşıya varılamamış olduğudur) listeyi şu şekilde verebiliriz (Bondi ve Samuel, 1997):
Mach 0. Evren, uzaktaki galaksilerin ortalama hareketiyle temsil edildiği üzere, yerel eylemsiz çerçevelere göre dönmez.
Mach 1. Newton’ın kütleçekim sabiti, G, dinamik bir alandır.
Mach 2. Boş bir uzayda bulunan cismin eylemsizliği yoktur.
Mach 3. Yerel eylemsizlik çerçeveleri kozmik hareketten öyle etkilenmiştir ki evrendeki maddenin ortalama hareketi yerel eylemsiz çerçevelerine göre dönmez şekilde görülür.
Mach 4. Evren uzaysal olarak kapalıdır.
Mach 5. Evrenin toplam açısal momentumu, momentumu ve enerjisi sıfırdır.
Mach 6. Maddenin eylemsizliğini evrendeki madde dağılımı belirler.
Mach 7. Evrendeki tüm maddeyi alırsanız, uzay da kalmaz.
Mach 8. Bu sayı bir mertebesinde kesin bir sayıdır. Burada evrenin ortalama yoğunluğu, Newton’ın kütleçekim sabiti ve Hubble zamanıdır.
Mach 9. Mutlak hiçbir yapı yoktur.
Mach 10. Sistemin geneline yapılan ötelemeler ve döndürmeler gözlemlenemezdir.
Bunlar literatürde olanlardan bazıları. Bizim favorimiz olan tanımı vermeden önce bazı matematiksel kavramları açmamız gerekir.
Ayar simetrisi (gauge symmetry): Bir kuramın fiziksel olmayan simetrilerine verilen addır. Yani bir kuramda bazı ayar dönüşümleri yapıyorsak ve gözlemlenebilen fiziksel nicelikler bundan etkilenmiyorsa deriz ki kuram belirli bir ayar simetrisine sahiptir. Örneğin Newton’ın klasik mekaniği tüm evrenin ötelemeleri altında simetriktir. Yani bütün evrendeki maddeyi bir metre yukarı (bunun yerine kendi favori yönünüzü de seçebilirsiniz) taşıdığımızda evren yine bildiğimiz evrendir. Hiçbir şey değişmemiştir. Onun için Newton mekaniğinin öteleme simetrisi vardır diyebiliriz.
Ayar grubu (gauge group): Ayar dönüşümlerinin oluşturduğu gruptur. Bunun için ayar dönüşümlerinin bazı özellikleri sağlaması gerekir (bunlara grup belitleri/aksiyomları denir):
- Birim eleman. Yani sisteme hiçbir işlem yapmayan bir simetri vardır.
- Ters eleman. Bir simetri dönüşümünün etkilerini geri alabilecek bir simetri dönüşümü vardır. Mesela Newton mekaniğinde tüm evreni bir metre yukarı kaydırdık. Sonra da bir metre aşağı kaydırdık. Aşağı kaydırma işlemi, yukarı kaydırma işleminin tersidir. Ve birbirine ters olan dönüşümlerin art arda uygulanması birim elemanı verir.
- Kapalılık. Art arda uygulanan ayar dönüşümlerinin de bir ayar dönüşümü olması gerekir.
- Birleşme özelliği. birer ayar dönüşümü olsun ve art arda uygulansın. ’dan önce ikilisini uygulamakla ’den sonra ikilisini uygulamak arasında fark yoktur. Matematiksel bir kesinlikle ifade edersek birleşme özelliği şu demektir: .
Konfigürasyon uzayı (configuration space): Bir kuramın izin verdiği tüm hallerin bir kümesidir, uzayıdır.
Denklik sınıfı (equivalence class): Bir kümenin birbirine denk (birbirine denk demek bir denklik bağıntısıyla birbirine bağlı olmak demektir) olan elemanlarının oluşturduğu kümedir.
Bizim (daha sonradan Şekil Dinamiği kuramını anlatırken kullanacağımız üzere) benimsediğimiz tanım ise Julian Barbour’a (2010) ait:
Şekil Dinamiği kuramına ileride daha detaylı olarak değineceğiz, fakat burada hemen şunu ifade edelim ki bu kuram Barbour’un Mach ilkesi yorumu (Mach 11) ile uyumludur. Fakat Newton mekaniği Mach 11 ile genelde (hemen hemen her zaman) uyumlu değildir. Burada kısacık da olsa Barbour tarafından ortaya atılan oyuncak bir Şekil Dinamiği kuramına değinelim.
Oyuncak Şekil Dinamiği kuramı, birbiriyle belirli kuvvetlerle etkileşen parçacıkları konu alır. Bu kuramda önemli olan parçacıkların birbirleri arasındaki mesafelerdir: yani Newton’ın mutlak uzayı üzerindeki koordinatları değil. Ayar simetrileri ise şöyledir: ötelemeler, döndürmeler, ve ölçek dönüşümleri. Bunları hemen birer örnekle açıklayalım:
1) Bütün evreni 1 metre yukarı ötelersek evren yine aynı evrendir
2) Evreni doksan derece döndürsek yine aynı evrene bakarız, evren yine aynı evrendir sadece bizim bakış açımız değişmiştir
3) Bütün evrendeki mesafeleri iki katına çıkartırsak, bu mesafeleri ölçeceğimiz metre çubuğunun da boyu iki katına çıkacaktır ve biz uzaklıkları yine aynı şekilde ölçeceğiz.
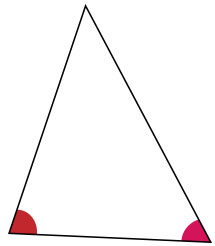 Örneğin üç tane parçacıktan oluşan bir evreni düşünelim. Üç parçacık bir üçgen oluştururlar. Oyuncak Şekil Dinamiği kuramına göre bu üçgenin uzaydaki yönelimi, konumu ve boyutu önemli değildir. Peki önemli olan nedir? Üçgendeki açılar! Bir üçgenin açıları, o üçgenin şeklini belirler. Şekil Dinamiği adı da buradan geliyor. Mach 11’e dönecek olursak, indirgenmiş konfigürasyon uzayımız üç parçacıklı evren için, bir açı çiftlerinden oluşur.
Örneğin üç tane parçacıktan oluşan bir evreni düşünelim. Üç parçacık bir üçgen oluştururlar. Oyuncak Şekil Dinamiği kuramına göre bu üçgenin uzaydaki yönelimi, konumu ve boyutu önemli değildir. Peki önemli olan nedir? Üçgendeki açılar! Bir üçgenin açıları, o üçgenin şeklini belirler. Şekil Dinamiği adı da buradan geliyor. Mach 11’e dönecek olursak, indirgenmiş konfigürasyon uzayımız üç parçacıklı evren için, bir açı çiftlerinden oluşur.
Eğer biz oyuncak Şekil Dinamiği kuramındaki parçacıkları Newton’ın mutlak uzayına koymak istersek bütün dinamiği Newton yasalarıyla uyumlu yazabiliriz fakat evren üzerinde bazı koşullar altında:
1) Evrenin toplam momentumunun sıfır olduğu koordinat çerçevesinde toplam açısal momentumu da sıfır olmalı. Eğer böyle olmasaydı evren bir şeyin için de dönüyor olacaktı ki bu da Newton’ın mutlak uzayını doğururdu. Fakat Şekil Dinamiğinde mutlak uzay yoktur.
2) Evrenin eylemsizlik momenti değişmez. Bunu evrenin büyüklüğünün değişmeyeceği şeklinde yorumlayabiliriz. Tabi ki burada sadece oyuncak bir modelden bahsediyoruz. Daha detaylı bir analiz için ileride yazacağımız tam Şekil Dinamiği kuramına ihtiyacımız olacak.
Bu yazıda neler öğrendik? Mach ilkesi üzerinde bir anlaşma sağlanabilmiş bir ilke değil: literatürde çokça yorum mevcut. Bunları sıraladık, ardından da bizim kullanacağımız yorumu matematiksel bir hazırlık yaparak verdik. Yazı dizimizin ana hattı olacak olan Şekil Dinamiği kuramı Barbour’un Mach ilkesi yorumuyla uyumludur. Şekil dinamiği için oyuncak bir kuramdan bahsettik. Burada birbirleriyle belirli kuvvetler aracılığıyla etkileşen parçacıklar var ve fiziksel değişkenlerimiz parçacıkların oluşturduğu şekillerdeki açılar. Bu oyuncak kuram da Barbour’un Mach ilkesi ile uyumludur. Eğer bu kuramı Mach ilkesi ile sorunlu olan Newton mekaniği cinsinden yazacak olursak bazı şartların sağlanması gerekir.
Mach 0. Evren, uzaktaki galaksilerin ortalama hareketiyle temsil edildiği üzere, yerel eylemsiz çerçevelere göre dönmez.
Mach 1. Newton’ın kütleçekim sabiti, G, dinamik bir alandır.
Mach 2. Boş bir uzayda bulunan cismin eylemsizliği yoktur.
Mach 3. Yerel eylemsizlik çerçeveleri kozmik hareketten öyle etkilenmiştir ki evrendeki maddenin ortalama hareketi yerel eylemsiz çerçevelerine göre dönmez şekilde görülür.
Mach 4. Evren uzaysal olarak kapalıdır.
Mach 5. Evrenin toplam açısal momentumu, momentumu ve enerjisi sıfırdır.
Mach 6. Maddenin eylemsizliğini evrendeki madde dağılımı belirler.
Mach 7. Evrendeki tüm maddeyi alırsanız, uzay da kalmaz.
Mach 8. Bu sayı bir mertebesinde kesin bir sayıdır. Burada evrenin ortalama yoğunluğu, Newton’ın kütleçekim sabiti ve Hubble zamanıdır.
Mach 9. Mutlak hiçbir yapı yoktur.
Mach 10. Sistemin geneline yapılan ötelemeler ve döndürmeler gözlemlenemezdir.
Bunlar literatürde olanlardan bazıları. Bizim favorimiz olan tanımı vermeden önce bazı matematiksel kavramları açmamız gerekir.
Ayar simetrisi (gauge symmetry): Bir kuramın fiziksel olmayan simetrilerine verilen addır. Yani bir kuramda bazı ayar dönüşümleri yapıyorsak ve gözlemlenebilen fiziksel nicelikler bundan etkilenmiyorsa deriz ki kuram belirli bir ayar simetrisine sahiptir. Örneğin Newton’ın klasik mekaniği tüm evrenin ötelemeleri altında simetriktir. Yani bütün evrendeki maddeyi bir metre yukarı (bunun yerine kendi favori yönünüzü de seçebilirsiniz) taşıdığımızda evren yine bildiğimiz evrendir. Hiçbir şey değişmemiştir. Onun için Newton mekaniğinin öteleme simetrisi vardır diyebiliriz.
Ayar grubu (gauge group): Ayar dönüşümlerinin oluşturduğu gruptur. Bunun için ayar dönüşümlerinin bazı özellikleri sağlaması gerekir (bunlara grup belitleri/aksiyomları denir):
- Birim eleman. Yani sisteme hiçbir işlem yapmayan bir simetri vardır.
- Ters eleman. Bir simetri dönüşümünün etkilerini geri alabilecek bir simetri dönüşümü vardır. Mesela Newton mekaniğinde tüm evreni bir metre yukarı kaydırdık. Sonra da bir metre aşağı kaydırdık. Aşağı kaydırma işlemi, yukarı kaydırma işleminin tersidir. Ve birbirine ters olan dönüşümlerin art arda uygulanması birim elemanı verir.
- Kapalılık. Art arda uygulanan ayar dönüşümlerinin de bir ayar dönüşümü olması gerekir.
- Birleşme özelliği. birer ayar dönüşümü olsun ve art arda uygulansın. ’dan önce ikilisini uygulamakla ’den sonra ikilisini uygulamak arasında fark yoktur. Matematiksel bir kesinlikle ifade edersek birleşme özelliği şu demektir: .
Konfigürasyon uzayı (configuration space): Bir kuramın izin verdiği tüm hallerin bir kümesidir, uzayıdır.
Denklik sınıfı (equivalence class): Bir kümenin birbirine denk (birbirine denk demek bir denklik bağıntısıyla birbirine bağlı olmak demektir) olan elemanlarının oluşturduğu kümedir.
Bizim (daha sonradan Şekil Dinamiği kuramını anlatırken kullanacağımız üzere) benimsediğimiz tanım ise Julian Barbour’a (2010) ait:
Mach 11. Bir fiziksel kuramın konfigürasyon uzayını düşünelim ve bunun üzerinde bir denklik bağıntısı kuralım: birbirine ayar dönüşümleriyle dönüşen tüm haller birbirine denktir. Elimizde bir denklik bağıntısı olduğuna göre artık konfigürasyon uzayımızı denklik sınıflarına ayırabiliriz. Bunu da yaptık diyelim. Sonra bu denklik sınıflarından birer tane eleman alarak indirgenmiş konfigürasyon uzayımızı oluşturalım. İndirgenmiş konfigürasyon uzayındaki her eleman birbirinden fiziksel olarak farklıdır; çünkü eğer böyle olmasaydı birbirlerine bir ayar dönüşümüyle dönüştürülebilirdi ki bu da onları baştaki büyük konfigürasyon uzayının içindeki aynı denklik sınıfına sokardı ve oradan bir temsilci seçeceğimiz zaman bir tanesini seçmek durumunda kalırdık. Şimdi istediğimiz uzaya eriştik. İndirgenmiş konfigürasyon uzayında eğer bir nokta ve bir yön ya da bir nokta ve bir teğet vektörü sistemin evrimini tek bir şekilde belirleyebiliyorsa bu kurama Mach ilkesiyle uyumlu denir.
Şekil Dinamiği kuramına ileride daha detaylı olarak değineceğiz, fakat burada hemen şunu ifade edelim ki bu kuram Barbour’un Mach ilkesi yorumu (Mach 11) ile uyumludur. Fakat Newton mekaniği Mach 11 ile genelde (hemen hemen her zaman) uyumlu değildir. Burada kısacık da olsa Barbour tarafından ortaya atılan oyuncak bir Şekil Dinamiği kuramına değinelim.
Oyuncak Şekil Dinamiği kuramı, birbiriyle belirli kuvvetlerle etkileşen parçacıkları konu alır. Bu kuramda önemli olan parçacıkların birbirleri arasındaki mesafelerdir: yani Newton’ın mutlak uzayı üzerindeki koordinatları değil. Ayar simetrileri ise şöyledir: ötelemeler, döndürmeler, ve ölçek dönüşümleri. Bunları hemen birer örnekle açıklayalım:
1) Bütün evreni 1 metre yukarı ötelersek evren yine aynı evrendir
2) Evreni doksan derece döndürsek yine aynı evrene bakarız, evren yine aynı evrendir sadece bizim bakış açımız değişmiştir
3) Bütün evrendeki mesafeleri iki katına çıkartırsak, bu mesafeleri ölçeceğimiz metre çubuğunun da boyu iki katına çıkacaktır ve biz uzaklıkları yine aynı şekilde ölçeceğiz.
 Örneğin üç tane parçacıktan oluşan bir evreni düşünelim. Üç parçacık bir üçgen oluştururlar. Oyuncak Şekil Dinamiği kuramına göre bu üçgenin uzaydaki yönelimi, konumu ve boyutu önemli değildir. Peki önemli olan nedir? Üçgendeki açılar! Bir üçgenin açıları, o üçgenin şeklini belirler. Şekil Dinamiği adı da buradan geliyor. Mach 11’e dönecek olursak, indirgenmiş konfigürasyon uzayımız üç parçacıklı evren için, bir açı çiftlerinden oluşur.
Örneğin üç tane parçacıktan oluşan bir evreni düşünelim. Üç parçacık bir üçgen oluştururlar. Oyuncak Şekil Dinamiği kuramına göre bu üçgenin uzaydaki yönelimi, konumu ve boyutu önemli değildir. Peki önemli olan nedir? Üçgendeki açılar! Bir üçgenin açıları, o üçgenin şeklini belirler. Şekil Dinamiği adı da buradan geliyor. Mach 11’e dönecek olursak, indirgenmiş konfigürasyon uzayımız üç parçacıklı evren için, bir açı çiftlerinden oluşur.Eğer biz oyuncak Şekil Dinamiği kuramındaki parçacıkları Newton’ın mutlak uzayına koymak istersek bütün dinamiği Newton yasalarıyla uyumlu yazabiliriz fakat evren üzerinde bazı koşullar altında:
1) Evrenin toplam momentumunun sıfır olduğu koordinat çerçevesinde toplam açısal momentumu da sıfır olmalı. Eğer böyle olmasaydı evren bir şeyin için de dönüyor olacaktı ki bu da Newton’ın mutlak uzayını doğururdu. Fakat Şekil Dinamiğinde mutlak uzay yoktur.
2) Evrenin eylemsizlik momenti değişmez. Bunu evrenin büyüklüğünün değişmeyeceği şeklinde yorumlayabiliriz. Tabi ki burada sadece oyuncak bir modelden bahsediyoruz. Daha detaylı bir analiz için ileride yazacağımız tam Şekil Dinamiği kuramına ihtiyacımız olacak.
Bu yazıda neler öğrendik? Mach ilkesi üzerinde bir anlaşma sağlanabilmiş bir ilke değil: literatürde çokça yorum mevcut. Bunları sıraladık, ardından da bizim kullanacağımız yorumu matematiksel bir hazırlık yaparak verdik. Yazı dizimizin ana hattı olacak olan Şekil Dinamiği kuramı Barbour’un Mach ilkesi yorumuyla uyumludur. Şekil dinamiği için oyuncak bir kuramdan bahsettik. Burada birbirleriyle belirli kuvvetler aracılığıyla etkileşen parçacıklar var ve fiziksel değişkenlerimiz parçacıkların oluşturduğu şekillerdeki açılar. Bu oyuncak kuram da Barbour’un Mach ilkesi ile uyumludur. Eğer bu kuramı Mach ilkesi ile sorunlu olan Newton mekaniği cinsinden yazacak olursak bazı şartların sağlanması gerekir.
Kaynak ve İleri Okuma
- Barbour, J. (2010). The definition of Mach’s principle. Foundations of Physics, 40(9-10), 1263-1284.
- Bondi, H., & Samuel, J. (1997). The Lense-Thirring effect and Mach's principle. Physics Letters A, 228(3), 121-126.";
Etiket
Projelerimizde bize destek olmak ister misiniz?
Dilediğiniz miktarda aylık veya tek seferlik bağış yapabilirsiniz.
Destek Ol
Yorum Yap (0)
Bunlar da İlginizi Çekebilir

31 Ağustos 2016
Gökada Oluşumunun Yükselişi ve Çöküşü

24 Aralık 2015
Şişme Evresinde Sicim İzleri Aranıyor

28 Ekim 2016
Hayır, Evren Hızlanarak Genişlemiyor!

04 Nisan 2018
Higgs Bozonlarının Gizli Yaşamı

14 Haziran 2018
Şekil Dinamiğine Giriş

09 Ekim 2019
2019 Nobel Fizik Ödülü