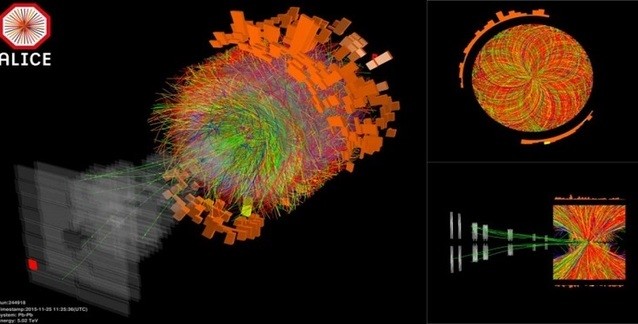
Büyük Hadron Çarpıştırıcısı'nın Keşiflerini Yetersiz Matematiğimiz mi Sınırlandıracak?
Protonları çarpıştırmak başka şey, çarpışmadan geriye kalan enkazdan bilimsel anlamlar çıkarmak başka şey. Peki acaba fizikçiler bir parçacık çarpışması sırasında gerçekte neler...
 Christian Gwiozda / Quanta Magazine
Christian Gwiozda / Quanta Magazine
Yıldız Teknik Üniversitesi - Çevirmen/Editör

Protonları çarpıştırmak başka şey, çarpışmadan geriye kalan enkazdan bilimsel anlamlar çıkarmak başka şey. Peki acaba fizikçiler bir parçacık çarpışması sırasında gerçekte neler olduğunu nasıl sonradan anlayabiliyor? Aslına bakarsanız, bazı durumlarda hesaplamalar o kadar güçleşiyor ki, yapamayabiliyorlar; tabi şimdilik.
Dünyadaki en büyük ve en güçlü parçacık hızlandırıcı olan Büyük Hadron Çarpıştırıcısı'na (LHC) ev sahipliği yapan CERN'de de böyle durumlar yaşanıyor. LHC'de gerçekleşen çarpışmalardan elde edilen verilerin bütününü anlamak için deneysel fizikçiler ve kuramsal fizikçiler sürekli birbirleri ile paslaşıyorlar.
Deneyciler, giderek daha da çetrefilli hâle gelen deneysel hedefler koyuyorlar; Higgs bozonun özelliklerini tam olarak ölçmek gibi. Böyle büyük hedefler ise çoğu zaman fazlasıyla emek isteyen kuramsal hesaplamalar gerektiriyor; bu iş de elbette kuramcılara düşüyor. İtalya'da bulunan Padua Üniversitesi'nden kuramsal fizikçi Pierpaolo Mastrolia şöyle diyor: "Deneycilerin istek listesi her zaman çok sayıda karmaşık süreçle dolu olur. O nedenle biz makul zaman zarfları içinde hesaplanabilecek olanları belirliyoruz."
Mastrolia'nın burada sözünü ettiği "süreçler" parçacıkların çarpışmasıyla birlikte gelişen olaylar zinciri oluyor. Örneğin bir çift gluon, bir dizi ara basamaktan geçirilerek Higgs bozonu oluşturulabilir ve ardından o da başka parçacıklara bozunur. Genellikle fizikçiler çok sayıda parçacıkla ilgili süreçleri incelemeyi yeğler. Çünkü karmaşıklık arttıkça, günümüzdeki en iyi kuramlarla tanımlanamayan kimi fiziksel etkilerin araştırılması desteklenir. Öte yandan parçacık sayısı arttıkça, işin matematiği de güçleşir.
Böyle hesaplamaları gerçekleştirmek için fizikçiler "Feynman diyagramı" adı verilen bir araç kullanır. Feynman diyagramları, çöp adam çizimlerini andıran çok yararlı hesap gereçleridir. Farklı tür parçacıklar farklı tür çizgilerle temsil edilir ve çizgilerin kesişim noktası çarpışmaya işaret eder. Kesişim noktasından öteye uzanan çizgilerin gösterdiği parçacıklar da, çarpışmadan sonra oluşan parçacıklar demektir.
Fizikçiler, bir deneyin başından sonuna dek izleyebileceği olası her yolun integralini alıp, bu integralleri toplar. Olası yolların sayısı arttıkça, kuramcıların hesaplaması gereken integral sayısı da artar; tabi her bir integral hesaplaması da güçleşir.
İnceleyecekleri çarpışma türlerine karar verirken, fizikçilerin iki ana seçim yapması gerekir. Birincisi, dikkate alacakları başlangıç durumu (giren) ve son durum (çıkan) parçacık sayısına karar vermelidirler. Çoğu deneyde iki tane gelen parçacık ve bir ilâ bri düzine arasında değişen çıkan parçacık olur. Bunlar Feynman diyagramında "bacaklar" (İng. legs) olarak adlandırılır.
İkinci olarak ise hesaba katacakları "düğüm" (İng. loop) sayısına karar vermeleri gerekir. Diyagramda düğümler, başlangıç durumu ile son durum arasında gerçekleşen tüm ara çarpışmaları temsil eder. Daha fazla düğüm eklemek, ölçümün doğruluğunu yükseltirken, diyagram hesaplamalarına dikkate değer yükler bindirir. Genel anlamda, düğümler ile bacaklar arasında karşılıklı ödünleşme vardır: Eğer hesaba daha fazla düğüm katmak istiyorsanız, daha az bacak dikkate almanız gerekir. Eğer daha fazla bacak dikkate almak isteğindeyseniz, az sayıda düğümle sınırlı kalmanız gerekir.
CERN kuramsal fizikçilerinden Gavin Salam şöyle diyor: "Eğer iki düğüm alırsanız, alabileceğiniz en fazla bacak sayısı iki olur. İki düğüme giren üç parçacık almayı deneyenler oldu; şu anda tekniğin en gelişkin düzeyinin ötesindeki sınır bu."
Fizikçiler şu anda üçüncü seviye (sıfır düğüm) olasılıkları ve herhangi bir sayıda giren parçacığın olduğu tek düğümlü diyagramları hesaplayacak araçlara sahipler. Ancak daha fazla düğümü hesaba katmak, hâlâ çok güç bir iş ve nihayetinde LHC'de başarılabilecek keşifler için limit koyucu etken bu olabilir.
"Bir parçacık keşfettiğimizde ve onun spin, kütle, açısal momentum ya da diğer parçacıklarla çiftlenme gibi özelliklerini belirlemek istediğimizde, düğümlerin olduğu yüksek mertebeli hesaplamalar gerekli hâle geliyor," diyor Mastrolia.
Feynman diyagramları ile sayı kuramı arasında beliren bağlantıların çoğu kişiyi heyecanlandırmasının nedeni işte bu. Eğer matematikçiler ve fizikçiler, iki ya da daha fazla düğümlü diyagramlar için üretilen değerlerde desenler belirleyebilirse, hesaplamaları çok daha basitleşebilir. Böylece deneyciler de en fazla ilgilerini çeken türde çarpışmaları incelemek için gereksinim duydukları matematiğe sahip olabilirler.
Dünyadaki en büyük ve en güçlü parçacık hızlandırıcı olan Büyük Hadron Çarpıştırıcısı'na (LHC) ev sahipliği yapan CERN'de de böyle durumlar yaşanıyor. LHC'de gerçekleşen çarpışmalardan elde edilen verilerin bütününü anlamak için deneysel fizikçiler ve kuramsal fizikçiler sürekli birbirleri ile paslaşıyorlar.
Feynman Diyagramları
Deneyciler, giderek daha da çetrefilli hâle gelen deneysel hedefler koyuyorlar; Higgs bozonun özelliklerini tam olarak ölçmek gibi. Böyle büyük hedefler ise çoğu zaman fazlasıyla emek isteyen kuramsal hesaplamalar gerektiriyor; bu iş de elbette kuramcılara düşüyor. İtalya'da bulunan Padua Üniversitesi'nden kuramsal fizikçi Pierpaolo Mastrolia şöyle diyor: "Deneycilerin istek listesi her zaman çok sayıda karmaşık süreçle dolu olur. O nedenle biz makul zaman zarfları içinde hesaplanabilecek olanları belirliyoruz."
Mastrolia'nın burada sözünü ettiği "süreçler" parçacıkların çarpışmasıyla birlikte gelişen olaylar zinciri oluyor. Örneğin bir çift gluon, bir dizi ara basamaktan geçirilerek Higgs bozonu oluşturulabilir ve ardından o da başka parçacıklara bozunur. Genellikle fizikçiler çok sayıda parçacıkla ilgili süreçleri incelemeyi yeğler. Çünkü karmaşıklık arttıkça, günümüzdeki en iyi kuramlarla tanımlanamayan kimi fiziksel etkilerin araştırılması desteklenir. Öte yandan parçacık sayısı arttıkça, işin matematiği de güçleşir.
Böyle hesaplamaları gerçekleştirmek için fizikçiler "Feynman diyagramı" adı verilen bir araç kullanır. Feynman diyagramları, çöp adam çizimlerini andıran çok yararlı hesap gereçleridir. Farklı tür parçacıklar farklı tür çizgilerle temsil edilir ve çizgilerin kesişim noktası çarpışmaya işaret eder. Kesişim noktasından öteye uzanan çizgilerin gösterdiği parçacıklar da, çarpışmadan sonra oluşan parçacıklar demektir.
İntegraller Güçleşiyor
Fizikçiler, bir deneyin başından sonuna dek izleyebileceği olası her yolun integralini alıp, bu integralleri toplar. Olası yolların sayısı arttıkça, kuramcıların hesaplaması gereken integral sayısı da artar; tabi her bir integral hesaplaması da güçleşir.
İnceleyecekleri çarpışma türlerine karar verirken, fizikçilerin iki ana seçim yapması gerekir. Birincisi, dikkate alacakları başlangıç durumu (giren) ve son durum (çıkan) parçacık sayısına karar vermelidirler. Çoğu deneyde iki tane gelen parçacık ve bir ilâ bri düzine arasında değişen çıkan parçacık olur. Bunlar Feynman diyagramında "bacaklar" (İng. legs) olarak adlandırılır.
İkinci olarak ise hesaba katacakları "düğüm" (İng. loop) sayısına karar vermeleri gerekir. Diyagramda düğümler, başlangıç durumu ile son durum arasında gerçekleşen tüm ara çarpışmaları temsil eder. Daha fazla düğüm eklemek, ölçümün doğruluğunu yükseltirken, diyagram hesaplamalarına dikkate değer yükler bindirir. Genel anlamda, düğümler ile bacaklar arasında karşılıklı ödünleşme vardır: Eğer hesaba daha fazla düğüm katmak istiyorsanız, daha az bacak dikkate almanız gerekir. Eğer daha fazla bacak dikkate almak isteğindeyseniz, az sayıda düğümle sınırlı kalmanız gerekir.
CERN kuramsal fizikçilerinden Gavin Salam şöyle diyor: "Eğer iki düğüm alırsanız, alabileceğiniz en fazla bacak sayısı iki olur. İki düğüme giren üç parçacık almayı deneyenler oldu; şu anda tekniğin en gelişkin düzeyinin ötesindeki sınır bu."
LHC'nin Kapasitesinden Yararlanmak İçin Matematik Gerek
Fizikçiler şu anda üçüncü seviye (sıfır düğüm) olasılıkları ve herhangi bir sayıda giren parçacığın olduğu tek düğümlü diyagramları hesaplayacak araçlara sahipler. Ancak daha fazla düğümü hesaba katmak, hâlâ çok güç bir iş ve nihayetinde LHC'de başarılabilecek keşifler için limit koyucu etken bu olabilir.
"Bir parçacık keşfettiğimizde ve onun spin, kütle, açısal momentum ya da diğer parçacıklarla çiftlenme gibi özelliklerini belirlemek istediğimizde, düğümlerin olduğu yüksek mertebeli hesaplamalar gerekli hâle geliyor," diyor Mastrolia.
Feynman diyagramları ile sayı kuramı arasında beliren bağlantıların çoğu kişiyi heyecanlandırmasının nedeni işte bu. Eğer matematikçiler ve fizikçiler, iki ya da daha fazla düğümlü diyagramlar için üretilen değerlerde desenler belirleyebilirse, hesaplamaları çok daha basitleşebilir. Böylece deneyciler de en fazla ilgilerini çeken türde çarpışmaları incelemek için gereksinim duydukları matematiğe sahip olabilirler.
Kaynak ve İleri Okuma
- Nautilus, "The Math That’s Too Difficult for Physics" ";
Etiket
Projelerimizde bize destek olmak ister misiniz?
Dilediğiniz miktarda aylık veya tek seferlik bağış yapabilirsiniz.
Destek Ol
Yorum Yap (0)
Bunlar da İlginizi Çekebilir

25 Ocak 2016
Nötrino Kendi Kendisinin Antiparçacığı mı?

06 Nisan 2015
Penguen Anomalisi Bilinmeyen Parçacıklara İşaret Ediyor

27 Haziran 2021
"OMG" Parçacığı Nedir? Nereden Geliyor?

04 Nisan 2018
Higgs Bozonlarının Gizli Yaşamı
26 Temmuz 2016
Gama Işınları Hakkında 7 Önemli Bilgi