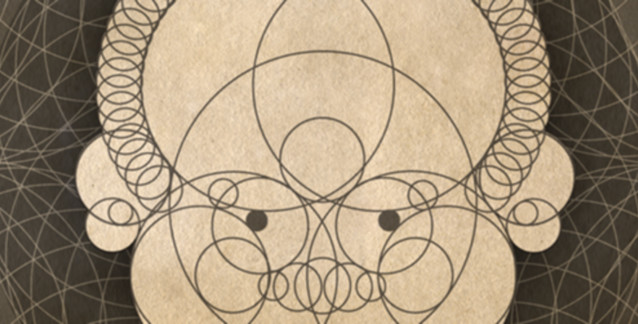
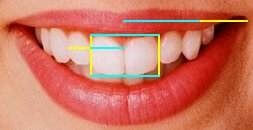
 Bu yapıyı kozalaklardan ananaslara kadar pek çok başka nesnede görmek mümkün. Ayrıca hayvanlar aleminde de, canlıların iskelet yapılarında ve uzuvların yerleşiminde rastlanıyor. Örneğin üst çenedeki ön iki dişin enlerinin toplamının boylarına oranı, altın orana ne kadar yakınsa göze o kadar hoş görünür. 17.yüzyıl matematikçilerinden Adolf Zeising, bitkilerde altın oranı tespit ettikten sonra, insan bedeninde de aynı orana pek çok yerde rastladığını 1854 tarihinde açıklamıştı. İdeal görüntüyü sağlayacak olan bu oranlara şu örnekleri verebiliriz: Yüzün boyu/ yüzün genişliği, dudak-kaşların birleşim yeri arası/ burun boyu, yüzün boyu/ çene ucu-kaşların birleşim yeri arası, ağız boyu/ burun genişliği, burun genişliği/ burun delikleri arası, parmak ucu-dirsek arası/ el bileği-dirsek arası, omuz hizasından baş ucuna olan mesafe/ kafa boyu, göbek-baş ucu arası mesafe/ omuz hizasından baş ucuna olan mesafe, göbek-diz arası/ diz-ayak ucu arası.
Bu yapıyı kozalaklardan ananaslara kadar pek çok başka nesnede görmek mümkün. Ayrıca hayvanlar aleminde de, canlıların iskelet yapılarında ve uzuvların yerleşiminde rastlanıyor. Örneğin üst çenedeki ön iki dişin enlerinin toplamının boylarına oranı, altın orana ne kadar yakınsa göze o kadar hoş görünür. 17.yüzyıl matematikçilerinden Adolf Zeising, bitkilerde altın oranı tespit ettikten sonra, insan bedeninde de aynı orana pek çok yerde rastladığını 1854 tarihinde açıklamıştı. İdeal görüntüyü sağlayacak olan bu oranlara şu örnekleri verebiliriz: Yüzün boyu/ yüzün genişliği, dudak-kaşların birleşim yeri arası/ burun boyu, yüzün boyu/ çene ucu-kaşların birleşim yeri arası, ağız boyu/ burun genişliği, burun genişliği/ burun delikleri arası, parmak ucu-dirsek arası/ el bileği-dirsek arası, omuz hizasından baş ucuna olan mesafe/ kafa boyu, göbek-baş ucu arası mesafe/ omuz hizasından baş ucuna olan mesafe, göbek-diz arası/ diz-ayak ucu arası.
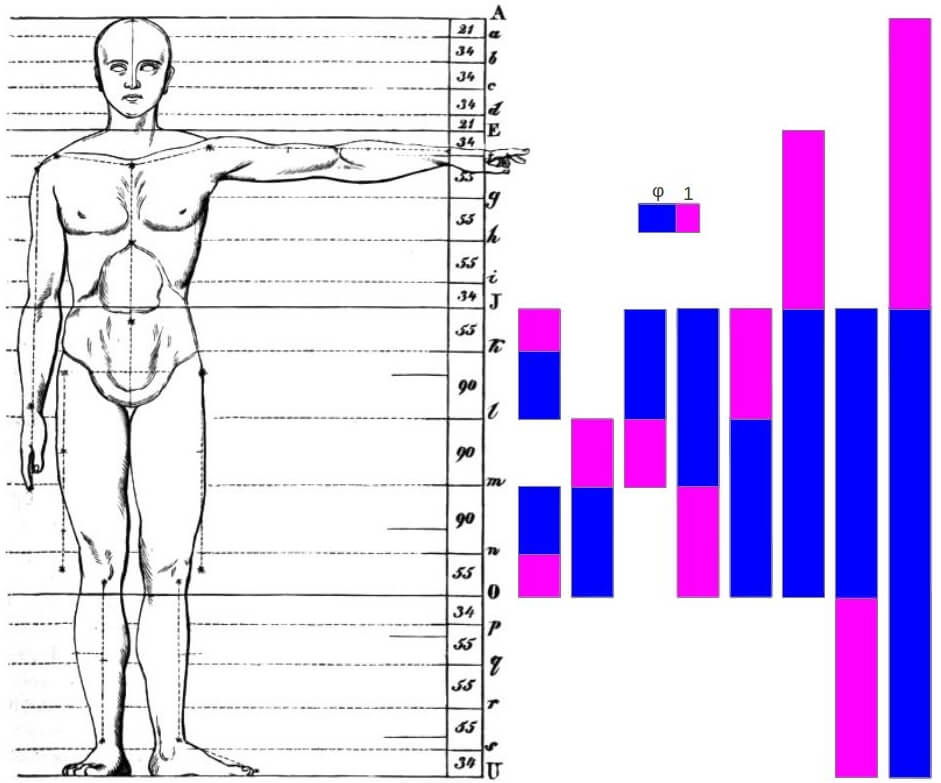 İnsan bedeninde Zeising tarafından bulunan altın oranlar.
İnsan bedeninde Zeising tarafından bulunan altın oranlar.Nasıl ki her insanın bedenindeki her oran bu ideallere uymuyorsa, çiçeklerin de Fibonacci dizisinden farklı yapılar sergiledikleri olur. Geçtiğimiz günlerde Royal Society Open Science dergisinde yayımlanan bir makalede, günebakan çiçeklerinin göbeğindeki ay çekirdeği sarmallarının ne ölçüde Fibonacci dizilimine uyduğunu inceleyen bir çalışmanın sonuçları yayımlandı. Manchester Bilim ve Endüstri Müzesi'nin desteklediği, halk katılımıyla gerçekleştirilen Turing'in Ay Çiçekleri projesinden elde edilen bulgulara göre, incelenen 657 ay çiçeğinin (Lat. Helianthus annuus) yaklaşık beşte birinin Fibonacci sarmallaşması dışında yapılandığı saptandı. Bu çiçeklerin bir bölümü bütünüyle Fibonacci dışı dizilime sahipken, diğerlerinin de daha karmaşık sarmallaştıkları görüldü.
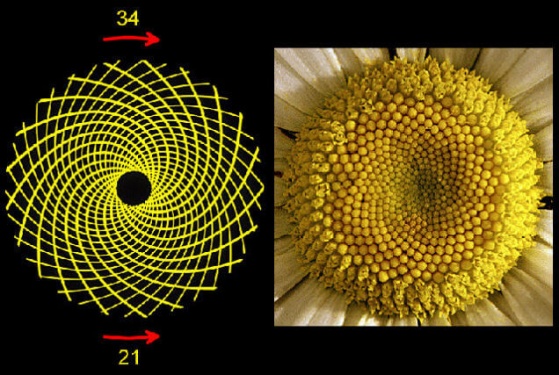 Bir papatyanın göbeğindeki sarmallarda bulunan Fibonacci sayıları.
Bir papatyanın göbeğindeki sarmallarda bulunan Fibonacci sayıları.Mimaride ve Sanatta Altın Oran
Tarih boyunca insanlar, icat yaparken çoğu zaman doğadan esinlenmişlerdir. Bu esinlenme sadece doğanın mekanik işleyişi ile sınırlı değildir aslında. Geçmişten günümüze en çok beğenilen mimari eserler ve sanat yapıtları incelendiğinde, neredeyse bütününde altın orana uyulduğu görülebilir.
Özellikle Altın Dikdörtgene (eni ile boyu arasındaki oran, altın orana uyan dikdörtgen) birçok yapı ve yapıtta sıkça rastlanır. Örneğin Leonardo DaVinci'nin ünlü Mona Lisa'sının hem uzuvlarında hem de tablonun bütününde altın dikdörtgenler görülür. Hindistan'daki Taç Mahal'de, Yunanistan'daki Parthenon'da ve hatta Paris'teki Eyfel Kulesi'nde de altın oranı görmek mümkündür. Günümüzde de, insanların algısına elden geldiğince hitap etmeyi amaçlayan firmalar, logolarının ve ürün etiketlerinin tasarımında altın oranı göz önüne almayı ihmal etmiyor.
 Hindistan'da bulunan Taç Mahal, Yunanistan’da bulunan Parthenon ve Paris'te bulunan Eyfel.
Hindistan'da bulunan Taç Mahal, Yunanistan’da bulunan Parthenon ve Paris'te bulunan Eyfel.Kaynaklar:
- Science, "Sunflowers show complex Fibonacci sequences"
<http://www.sciencemag.org/news/2016/05/sunflowers-show-complex-fibonacci-sequences > - Sacred Geometry, "Phi in the human body"
< http://www.sacred-geometry.es/?q=en/content/phi-human-body > - Golden Number, "The Human Body and the Golden Ratio"
< http://www.goldennumber.net/human-body/ > - Yeşim Özge Salan, "İnsan Vücudunda Altın Oran"
< http://users.metu.edu.tr/e154682/insan.htm > - Adolf Zeising, "New theory of the proportions of the human body, developed from a basic morphological law which stayed hiherto unknown, and which permeates the whole nature and art, accompanied by a complete summary of the prevailing systems"
< http://www.bsb-muenchen-digital.de/%7Eweb/web1025/bsb10255661/images/index.html?l=de&digID=bsb10255661&v=2p&nav=0 >
İlgili Makale: Royal Society Open Science, "Novel Fibonacci and non-Fibonacci structure in the sunflower: results of a citizen science experiment"
< http://rsos.royalsocietypublishing.org/content/3/5/160091 >
Dilediğiniz miktarda aylık veya tek seferlik bağış yapabilirsiniz.
Destek OlBunlar da İlginizi Çekebilir