Sicim Kuramı Matematiğin Uzak Uçlarını Birleştiriyor
1978 yılında garip bir rastlantı matematikçi John McKay'in dikkatini çekti. Kendisi, "canavar grup" adı verilen çok büyük boyutlu cebirsel bir nesnenin yapısını göstermenin fark...
 Olena Shmahalo/Quanta Magazine
Olena Shmahalo/Quanta Magazine
Yıldız Teknik Üniversitesi - Çevirmen/Editör

1978 yılında garip bir rastlantı matematikçi John McKay'in dikkatini çekti. Kendisi, "canavar grup" adı verilen çok büyük boyutlu cebirsel bir nesnenin yapısını göstermenin farklı yolları üzerinde çalışmıştı. Matematikçiler bu gizemli varlıkta yeni bir tür simetri olduğunu düşünüyorlardı. Canavar grubun gerçekte var olduğundan emin değillerdi ama eğer varsa bazı belli boyutlarda özel davranışlar sergileyecekti. Bu boyutlardan ilk ikisi 1 ve 196.883 idi. Kanada'nın Montreal kentinde bulunan Concordia Üniversitesi'nden McKay, bütünüyle farklı bir matematik dalına ilişkin bir makaleye denk gelmişti. Makale sayılar kuramının temel nesnelerinden j-fonksiyon ile ilgiliydi. Garip bir biçimde bu fonksiyonun ilk önemli katsayısı 196.884 idi. McKay bu sayının, canavarın ilk iki özel boyutunun toplamı olduğunu hemen fark etti.
Çoğu matematikçi bunun şans eseri olduğunu düşünüp görmezden geldi; çünkü canavar ile j-fonksiyonun uzaktan bile alakalı olmalarını beklemek için hiç bir neden yoktu. Ama bağlantı Florida Üniversitesi'nden Field Madalyası sahibi matematikçi John Thompson'un ilgisini çekmeyi başardı ve kendisi şu keşfi yaptı: j-fonksiyonun ikinci katsayısı olan 21.493.760 canavarın ilk üç özel boyutunun toplamıydı (1+196.883+21.296.876). Görünüşe bakılırsa j-fonksiyon, ele geçmez canavar grubun yapısını bir biçimde kontrol ediyordu.
Kısa süre sonra başka matematikçiler tarafından buna benzer pek çok sayısal bağlantı gösterildi ve artık rastlantının ötesinde bir şeyler olduğu açıklığa kavuştu. Sonrasında 1053'den fazla elemanı olan canavar grup yapılandırıldı. İlerleyen yıllarda California Üniversitesi'nden Richard Borcherds bu alandaki bir çalışması ile Field Madalyası aldı. Borcherds, canavar ile j fonksiyonun var olduğu iki uzak matematik bölgesi arasında bir köprü olduğunu kanıtladı: Sicim Kuramı.
Borcherd'in keşfi matematikte bir devrim tetikleyerek, genelleştirilmiş Kac-Moody cebirleri olarak bilinen yeni bir alanın doğmasına yol açtı. Ama sicim kuramı cephesinden bakınca, bunun pek de ilgi çekici yanı yoktu. Canavar ile j-fonksiyonu bağlantılandıran 24 boyutlu model, sicim kuramcılarının ilgilendiği modellerden değildi. Stanford Ünversitesi'nden sicim kuramı üzerinde çalışan Shamit Kachru şöyle diyor: "Bu kuramın ezoterik taraflarından biri gibiydi; pek fiziksel ilginçliği yoktu ama matematiksel sonuçlar şaşırtıcıydı."
Son beş yılda ise bunun hikâyenin sadece başlangıcı olduğu, sicim kuramına ilişkin derin ipuçları içerdiği anlaşıldı. 2012 yılında formüle edilen ve buna benzer 23 tane daha ilişkinin olduğunu ileri süren bir makalenin sayısal kanıtı geçtiğimiz hafta John Duncan, Michael Griffin ve Ken Ono tarafından yayımlandı. Bir simetri grubunun boyutları ile özel bir fonksiyonun katsayıları arasında saptanan bu 23 yeni bağlantı, sicim kuramının merkezinde yer alan en önemli yapılardan bazılarıyla iç içe geçmiş gibi görünüyor. Bu yapılar K3 yüzeyleri olarak bilinen 4-boyutlu nesneler. Amsterdam Üniversitesi'nden Miranda Cheng, bağlantıların bu yüzeylerde gizli simetrilere işaret ettiğini belirtiyor.
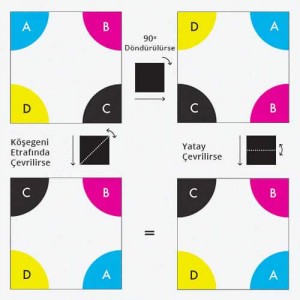
Her bir simetrinin kendine ait doğal bir aritmetiği olur. Örneğin bir kareyi 90 derece döndürdükten sonra yatay çevirmek, onu bir köşegeni etrafında çevirmekle aynı sonucu doğurur. 19.yüzyıl matematikçileri bu tür aritmetikleri "grup" adı verilen cebirsel nesnelerden çıkarabileceklerinin farkına vardı. Aynı soyut grup çok sayıda farklı şeklin simetrisini temsil edebiliyordu; bu da matematikçilerin farklı şekillerdeki ortak yanları anlamaları için net bir yol sağlıyordu. 20.yüzyılın büyük bölümü tüm olası grupların sınıflandırması çalışmaları ile geçti. Yavaş yavaş garip bir şey keşfedildi: Basit sonlu grupların çoğu doğal kategorilere ayrılırken, 26 tanesi kategorize edilemiyordu. Bunların en büyüğü ve en son keşfedileni canavardı.
McKay'ın neredeyse 40 yıl önceki rastlantısal keşfinden önce canavar grup ile j-fonksiyonun herhangi bir ortak yanı olacağı akla gelmezdi. Özel bir fonksiyon sınıfından olan j-fonksiyonun grafiği, tıpkı Escher'in çizimlerindeki yinelenen ve sınırlara yaklaşırken küçülen desenlere benzer. Bu "modüler (modular) foksiyonlar" sayılar kuramının kahramanlarıdır. "Sayılar kuramında ne zaman çarpıcı bir sonuç elde edildiğini duysanız, büyük olasılıkla modüler formlarla ilgili bir ifadedir bu aslında," diyor Kachru. Tıpkı bir ses dalgasında olduğu gibi, j-fonksiyonun yinelenen deseni saf tonların topluluğu olarak düşünülebilir. Katsayıların da her bir tonun ne kadar "yüksek" olduğunu gösterdiği söylenebilir. McKay'in bulduğu canavar grup bağlantısı işte bu katsayılarda saklıydı.
Borcherds hem j-fonksiyonun hem de canavar grubun rol oynadığı belli bir sicim kuramı modeli olduğunu göstererek, McKay'in keşfine anlam kazandırdı. Her bir enerji düzeyindeki sicimlerin yapabildiği salınım biçimlerinin sayısı, j-fonksiyonun katsayıları oluyordu. Canavar grup da modelin bu enerji düzeylerindeki simetrisini kapsıyordu. Keşif, akıllara durgunluk verecek büyüklükteki canavar grubun, katsayıları kolayca hesaplanabilen j-fonksiyon vasıtasıyla incelenmesi için matematikçilere bir yöntem sağladı.
Bu arada sicim kuramcıları farklı bir soruna odaklanmıştı: Sicimlerin var olduğu öne sürülen minik boyutların geometrisini ortaya çıkarmak. Farklı geometriler, sicimlerin farklı titreşimleri demekti; tıpkı farklı delikleri kapatılan flütün iç geometrisindeki değişim dolayısıyla farklı notalar vermesi gibi. Fizikçiler yıllar boyunca, gözlemlediğimiz dünyadaki etkileri yaratan bir geometri bulmayı denedi. K3 yüzeyler topluluğu, böyle bir geometrinin ümit vaad eden adaylarından birinin önemli bileşenlerindendi. Her bir enerji düzeyindeki sicimlerin titreşim türü sayılarını verecek kadar K3 geometrisi bilinmiyordu. Ama fizikçiler daha sınırlı bir fonksiyon yazabilir ve tüm K3 yüzeylerinde beliren fiziksel özellikleri sayabilirlerdi.
2010 yılında bir Japon araştırma ekibi şunun farkına vardı: Fonksiyonu belli bir biçimde yazdıklarında ortaya çıkan katsayılar, yaklaşık 250 milyon elemanı olan bir başka kategorisiz grubun, yani M24'ün özel boyutları ile bağlantılı oluyordu. Bu kez hem fizikçiler hem de matematikçiler keşfe büyük ilgi gösterdi. Çalışmanın ilerletilmesi ile tüm kategorize edilemeyen gruplar için böyle özel fonksiyonlar olduğu ve hepsinde de canavar durumundakine benzer bağlantılar olduğu anlaşıldı. Her birine karşılık gelen bir sicim kuramı vardı ve fonksiyon sicim durumlarını sayarken, grup ise modelin simetrisini sergiliyordu. Buluşun bu şekilde netleştirilmesi matematiğin efsanevi isimlerinden Ramanujan'ın bir çalışması sayesinde oldu.
Hindistan'da muhasebecilik yaparken İngiliz matematikçi G.H.Hardy'e gönderdiği mektup ile dehâsı anlaşılan Ramanujan keşiflerini tanrıça Namagiri'ye atfederken, matematik kariyeri çok kısa sürebildi. 1920'de, sadece 32 yaşında hayata veda eden Hintli dâhi, Hardy'e gönderdiği mektupların birinde "yapay teta (mock theta) fonsiyonlarını" keşfettiğini açıklamıştı. Bu fonksiyonlara 17 tane örnek yazmış, fakat bunların ortak yönünden söz etmemişti. Bu durum, 2002 yılında Sander Zwegers örneklerin, sonradan "yapay modüler (mock modular) formlar" adı verilecek olan nesneler olduğunu ortaya çıkarana dek, seksen yıldan uzun bir süre akılları kurcaladı. İşte kategorize edilemeyen grupların her biri bu yapay modüler formların katsayıları ile bağlantılıydı.
Duncan, Ono ve Griffin'in son makalesinde sunulan analiz, gruplar ile yapay modüler formları birleştiren sicim kuramlarını nerede aramaları gerektiğine ilişkin fizikçilere ipucu veriyor. Fizikçileri heyecanlandıran bir başka olasılık ise çalışmanın, kuantum mekaniği ile genel göreliliği birleştirip kuantum kütleçekim kuramı elde etme yolunda da yardımcı olabilecek olması.
Şöyle ki, 2007 yılında Princeton'dan ünlü sicim kuramcısı Edward Witten, bu çalışmaların üç boyutlu kuantum kütleçekim modeli yapılandırılmasında bir yol sağlayabileceğini ve canavar gruptaki 194 elemanın, kara deliklerin 194 sınıfına karşılık gelebileceğini ortaya atmıştı. Duncan yaptıkları son çalışma ile elde ettikleri sayısal kanıtın çok güçlü olduğunu vurgulayarak, fizikçilerden gelecek keşifleri beklediklerini ekliyor.
Çoğu matematikçi bunun şans eseri olduğunu düşünüp görmezden geldi; çünkü canavar ile j-fonksiyonun uzaktan bile alakalı olmalarını beklemek için hiç bir neden yoktu. Ama bağlantı Florida Üniversitesi'nden Field Madalyası sahibi matematikçi John Thompson'un ilgisini çekmeyi başardı ve kendisi şu keşfi yaptı: j-fonksiyonun ikinci katsayısı olan 21.493.760 canavarın ilk üç özel boyutunun toplamıydı (1+196.883+21.296.876). Görünüşe bakılırsa j-fonksiyon, ele geçmez canavar grubun yapısını bir biçimde kontrol ediyordu.
Canavar ile j'yi bağlayan sicim
Kısa süre sonra başka matematikçiler tarafından buna benzer pek çok sayısal bağlantı gösterildi ve artık rastlantının ötesinde bir şeyler olduğu açıklığa kavuştu. Sonrasında 1053'den fazla elemanı olan canavar grup yapılandırıldı. İlerleyen yıllarda California Üniversitesi'nden Richard Borcherds bu alandaki bir çalışması ile Field Madalyası aldı. Borcherds, canavar ile j fonksiyonun var olduğu iki uzak matematik bölgesi arasında bir köprü olduğunu kanıtladı: Sicim Kuramı.
Borcherd'in keşfi matematikte bir devrim tetikleyerek, genelleştirilmiş Kac-Moody cebirleri olarak bilinen yeni bir alanın doğmasına yol açtı. Ama sicim kuramı cephesinden bakınca, bunun pek de ilgi çekici yanı yoktu. Canavar ile j-fonksiyonu bağlantılandıran 24 boyutlu model, sicim kuramcılarının ilgilendiği modellerden değildi. Stanford Ünversitesi'nden sicim kuramı üzerinde çalışan Shamit Kachru şöyle diyor: "Bu kuramın ezoterik taraflarından biri gibiydi; pek fiziksel ilginçliği yoktu ama matematiksel sonuçlar şaşırtıcıydı."
Bağlantılar simetri işareti
Son beş yılda ise bunun hikâyenin sadece başlangıcı olduğu, sicim kuramına ilişkin derin ipuçları içerdiği anlaşıldı. 2012 yılında formüle edilen ve buna benzer 23 tane daha ilişkinin olduğunu ileri süren bir makalenin sayısal kanıtı geçtiğimiz hafta John Duncan, Michael Griffin ve Ken Ono tarafından yayımlandı. Bir simetri grubunun boyutları ile özel bir fonksiyonun katsayıları arasında saptanan bu 23 yeni bağlantı, sicim kuramının merkezinde yer alan en önemli yapılardan bazılarıyla iç içe geçmiş gibi görünüyor. Bu yapılar K3 yüzeyleri olarak bilinen 4-boyutlu nesneler. Amsterdam Üniversitesi'nden Miranda Cheng, bağlantıların bu yüzeylerde gizli simetrilere işaret ettiğini belirtiyor.
Her bir simetrinin kendine ait doğal bir aritmetiği olur. Örneğin bir kareyi 90 derece döndürdükten sonra yatay çevirmek, onu bir köşegeni etrafında çevirmekle aynı sonucu doğurur. 19.yüzyıl matematikçileri bu tür aritmetikleri "grup" adı verilen cebirsel nesnelerden çıkarabileceklerinin farkına vardı. Aynı soyut grup çok sayıda farklı şeklin simetrisini temsil edebiliyordu; bu da matematikçilerin farklı şekillerdeki ortak yanları anlamaları için net bir yol sağlıyordu. 20.yüzyılın büyük bölümü tüm olası grupların sınıflandırması çalışmaları ile geçti. Yavaş yavaş garip bir şey keşfedildi: Basit sonlu grupların çoğu doğal kategorilere ayrılırken, 26 tanesi kategorize edilemiyordu. Bunların en büyüğü ve en son keşfedileni canavardı.
Modüler fonsiyonlar ve kategori dışı gruplar
McKay'ın neredeyse 40 yıl önceki rastlantısal keşfinden önce canavar grup ile j-fonksiyonun herhangi bir ortak yanı olacağı akla gelmezdi. Özel bir fonksiyon sınıfından olan j-fonksiyonun grafiği, tıpkı Escher'in çizimlerindeki yinelenen ve sınırlara yaklaşırken küçülen desenlere benzer. Bu "modüler (modular) foksiyonlar" sayılar kuramının kahramanlarıdır. "Sayılar kuramında ne zaman çarpıcı bir sonuç elde edildiğini duysanız, büyük olasılıkla modüler formlarla ilgili bir ifadedir bu aslında," diyor Kachru. Tıpkı bir ses dalgasında olduğu gibi, j-fonksiyonun yinelenen deseni saf tonların topluluğu olarak düşünülebilir. Katsayıların da her bir tonun ne kadar "yüksek" olduğunu gösterdiği söylenebilir. McKay'in bulduğu canavar grup bağlantısı işte bu katsayılarda saklıydı.
Borcherds hem j-fonksiyonun hem de canavar grubun rol oynadığı belli bir sicim kuramı modeli olduğunu göstererek, McKay'in keşfine anlam kazandırdı. Her bir enerji düzeyindeki sicimlerin yapabildiği salınım biçimlerinin sayısı, j-fonksiyonun katsayıları oluyordu. Canavar grup da modelin bu enerji düzeylerindeki simetrisini kapsıyordu. Keşif, akıllara durgunluk verecek büyüklükteki canavar grubun, katsayıları kolayca hesaplanabilen j-fonksiyon vasıtasıyla incelenmesi için matematikçilere bir yöntem sağladı.
Bu arada sicim kuramcıları farklı bir soruna odaklanmıştı: Sicimlerin var olduğu öne sürülen minik boyutların geometrisini ortaya çıkarmak. Farklı geometriler, sicimlerin farklı titreşimleri demekti; tıpkı farklı delikleri kapatılan flütün iç geometrisindeki değişim dolayısıyla farklı notalar vermesi gibi. Fizikçiler yıllar boyunca, gözlemlediğimiz dünyadaki etkileri yaratan bir geometri bulmayı denedi. K3 yüzeyler topluluğu, böyle bir geometrinin ümit vaad eden adaylarından birinin önemli bileşenlerindendi. Her bir enerji düzeyindeki sicimlerin titreşim türü sayılarını verecek kadar K3 geometrisi bilinmiyordu. Ama fizikçiler daha sınırlı bir fonksiyon yazabilir ve tüm K3 yüzeylerinde beliren fiziksel özellikleri sayabilirlerdi.
2010 yılında bir Japon araştırma ekibi şunun farkına vardı: Fonksiyonu belli bir biçimde yazdıklarında ortaya çıkan katsayılar, yaklaşık 250 milyon elemanı olan bir başka kategorisiz grubun, yani M24'ün özel boyutları ile bağlantılı oluyordu. Bu kez hem fizikçiler hem de matematikçiler keşfe büyük ilgi gösterdi. Çalışmanın ilerletilmesi ile tüm kategorize edilemeyen gruplar için böyle özel fonksiyonlar olduğu ve hepsinde de canavar durumundakine benzer bağlantılar olduğu anlaşıldı. Her birine karşılık gelen bir sicim kuramı vardı ve fonksiyon sicim durumlarını sayarken, grup ise modelin simetrisini sergiliyordu. Buluşun bu şekilde netleştirilmesi matematiğin efsanevi isimlerinden Ramanujan'ın bir çalışması sayesinde oldu.
"Tanrıçanın yardımıyla" listelenen fonksiyonlar
Hindistan'da muhasebecilik yaparken İngiliz matematikçi G.H.Hardy'e gönderdiği mektup ile dehâsı anlaşılan Ramanujan keşiflerini tanrıça Namagiri'ye atfederken, matematik kariyeri çok kısa sürebildi. 1920'de, sadece 32 yaşında hayata veda eden Hintli dâhi, Hardy'e gönderdiği mektupların birinde "yapay teta (mock theta) fonsiyonlarını" keşfettiğini açıklamıştı. Bu fonksiyonlara 17 tane örnek yazmış, fakat bunların ortak yönünden söz etmemişti. Bu durum, 2002 yılında Sander Zwegers örneklerin, sonradan "yapay modüler (mock modular) formlar" adı verilecek olan nesneler olduğunu ortaya çıkarana dek, seksen yıldan uzun bir süre akılları kurcaladı. İşte kategorize edilemeyen grupların her biri bu yapay modüler formların katsayıları ile bağlantılıydı.
Duncan, Ono ve Griffin'in son makalesinde sunulan analiz, gruplar ile yapay modüler formları birleştiren sicim kuramlarını nerede aramaları gerektiğine ilişkin fizikçilere ipucu veriyor. Fizikçileri heyecanlandıran bir başka olasılık ise çalışmanın, kuantum mekaniği ile genel göreliliği birleştirip kuantum kütleçekim kuramı elde etme yolunda da yardımcı olabilecek olması.
Şöyle ki, 2007 yılında Princeton'dan ünlü sicim kuramcısı Edward Witten, bu çalışmaların üç boyutlu kuantum kütleçekim modeli yapılandırılmasında bir yol sağlayabileceğini ve canavar gruptaki 194 elemanın, kara deliklerin 194 sınıfına karşılık gelebileceğini ortaya atmıştı. Duncan yaptıkları son çalışma ile elde ettikleri sayısal kanıtın çok güçlü olduğunu vurgulayarak, fizikçilerden gelecek keşifleri beklediklerini ekliyor.
Kaynak ve İleri Okuma
- Erica Klarreich, Quanta Magazine, "Mathematicians Chase Moonshine’s Shadow" "; https://www.quantamagazine.org/20150312-mathematicians-chase-moonshines-shadow
- http://link.springer.com/article/10.1007%2FBF01389186
- http://link.springer.com/article/10.1007%2FBF01232032
- http://arxiv.org/abs/1204.2779
- http://arxiv.org/abs/1503.01472
- http://arxiv.org/abs/1004.0956
- http://dspace.library.uu.nl/handle/1874/878
- http://arxiv.org/pdf/0706.3359.pdf
Etiket
Projelerimizde bize destek olmak ister misiniz?
Dilediğiniz miktarda aylık veya tek seferlik bağış yapabilirsiniz.
Destek Ol
Yorum Yap (0)
Bunlar da İlginizi Çekebilir

12 Nisan 2016
Küre İstifleme Problemi 8 ve 24 Boyut İçin Çözüldü

26 Ekim 2018
Süpersicim Kuramına Genel Bir Bakış

23 Kasım 2015
Kuantum Kütleçekime İlişkin Temel Sorular

02 Ocak 2016
Her Şeyi Anlayabilir miyiz?

15 Haziran 2015
Fiziğin Çözülmemiş 9 Büyük Gizemi