Şişme Evresinde Sicim İzleri Aranıyor
Sicim kuramı sınanamazlığı ile ünlüdür. Fakat geçtiğimiz günlerde iki kuramsal fizikçininin ortaya attığı yöntem ile bu kurama ilişkin kanıt bulma umudu doğdu. İleri Araştırma E...
Sicim kuramı sınanamazlığı ile ünlüdür. Fakat geçtiğimiz günlerde iki kuramsal fizikçininin ortaya attığı yöntem ile bu kurama ilişkin kanıt bulma umudu doğdu. İleri Araştırma Enstitüsü'nden (IAS) kuramcılar, sicim kuramının sınanmasında ilerleme kaydedebilecek yöntemlerinin 14 milyar yıl önce varolan parçacıkları aramak üzerinde yoğunlaştığını ifade ediyor. O zamanlar evren, Büyük Hadron Çarpıştırıcısı'nda (LHC) gerçekleşen çarpışmalardan 15 milyar kat fazla enerjiyle büyümekteydi.
Bilimciler LHC'yi bu düzeye kadar çıkaramaz; hatta ona yaklaştıramaz bile. Ama teknolojinin yardımı ve evrenbilimsel çalışmalar aracılığıyla bu parçacıklara ilişkin kanıtları gözlemleme olasılıkları bulunur.
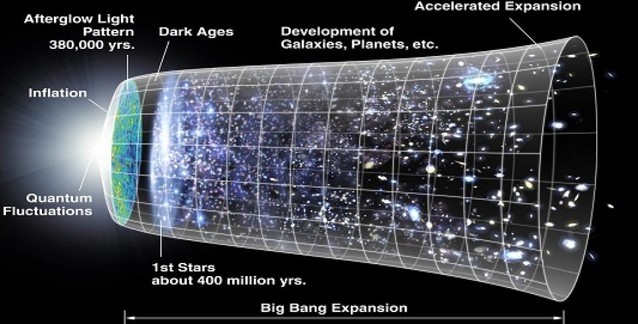
Şişme (Büyük Patlama'dan 10 ile 33 saniye arasında gerçekleşmiş olan çok kısa süreli aşırı evren büyümesi) sırasında parçacıklar astronomik ölçekte bir güçle çarpışıyorlardı. Bu zamana ait kalıntıları, kozmik arka alan ışınımı adını verdiğimiz kalıntı enerji sisindeki minik çalkantılar olarak görüyoruz. Bilimciler, o sıralarda varolan tarih öncesi parçacıkların kalıntılarını da belki bulabilir.
"Eğer şişme sırasında yeni parçacıklar varolduysa, ilkel çalkalanmalar üzerinde bir iz bırakmış olabilirler. Bunlar belirli desenler şeklinde göze çarpabilir," diyor Princeton İleri Araştırma Enstitüsü'nden kuramcı Juan Maldacena.
Maldacena ve çalışma arkadaşı Nima Arkani-Hamed, bu parçacık desenlerinin neye benzeyebileceği konusunda kuantum alan kuramı hesaplamaları yapmış ve elde ettikleri sonuçları, bu yıl Hindistan'da düzenlenen sicim kuramı konferansında sunmuşlardı.
Sicim kuramı genellikle en temel görüşü ile özetlenir: Maddenin temel birimleri parçacıklar değildir; tek boyutlu, titreşen enerji iplikçikleridir.
Kuramın amacı, kuantum mekaniği ile Einstein'ın genel görelilik kuramı arasındaki matematiksel bir uyuşmazlığı gidermektir. Örneğin bir kara deliğin içinde, kuantum mekaniğine göre kütleçekim imkansızdır. Bir kuramı diğerine uydurmak adına yapılan her türlü girişim, tüm narin sistemin çökmesine yol açar. Bunu denemek yerine, sicim kuramı yepyeni bir matematiksel çatı inşa eder. Bu yapıdan her iki kuram da doğal olarak doğar. Doğanın kuvvetleri zarif bir biçimde birleşir ve bilinen tüm temel parçacıklar doğru niteliklerle tanımlanmış olarak belirir.
Matematiksel bir sistem olarak sicim kuramı muazzam sayıda öngörüde bulunmuştur. Peki bunların ne kadarı test edilebilmiştir? Şimdiye kadar hiçbiri.
Sicimlerin evrendeki en küçük nesneler olduğu düşünülüyor. Parçacık fiziği deneylerindeki ölçekler bile sicimler için devasa büyüklükler anlamına geliyor. Dolayısıyla parçacık fiziği deneyleri üzerinde sicimlerin etkilerini hesaplamak hiç kolay değil. Sicim kuramcıları yeni parçacıkların varlığını öngörebiliyor, ama kütlelerini hesaplayamıyorlar.
Durumu daha da zorlaştıracak biçimde, sicim kuramı birbirlerinden kuvvet, parçacık ve boyut sayılarıyla farklılaşan çeşitli evrenler de tanımlayabiliyor. İncelenebilir enerjilerdeki öngörüler, bu bilinmeyen ayrıntılara bağlı oluyor. Hiçbir deney, gerçekliğin böylesine çoklu alternatifini sunan bir kuramı kanıtlayamaz.
Ama bilimciler sicim kuramını en azından kısmen test edebilecek deneyler yapabilmenin yollarını arıyor. Kuramın öngörülerinden biri, benzersiz bir özelliğe sahip parçacıkların varolduğu yönünde: Spini 2'den büyük olan parçacıklar.
Spin, temel parçacıkların bir özelliğidir. Spinsiz parçacıkların bozunumu simetrik desenler izler. Spinli parçacıkların bozunumu asimetrik olur ve spin arttıkça bu desenler giderek karmaşıklaşır. Böyle parçacıkların çarpışmalarından ortaya çıkan karmaşık bozunum desenleri, evren genişleyip soğurkenki duruma ilişkin izler barındırabilir.
Maldacena ve Arkani-Hamed'e göre, bilimciler spini 2'den büyük olan parçacıkların desenlerini, gökadaların dağılımının ince çeşitlemelerinde veya kozmik arka alan ışınımında bulabilir. Gözlemsel evrenbilimcilerin bu ufak sapmaları görebilmesi için geniş bir uzunluk ölçeği aralığında ilkel çalkalanmaları ölçmesi gerekir.
IAS kuramcıları, eğer böyle büyük kütleli ve yüksek spinli parçacıklar var ise ölçümlerin ne olması gerektiğini hesapladı. Böyle bir parçacığın, fizikçilerin LHC'de bulabileceğinden çok daha büyük kütleli olması gerekiyor.
Evrenbilimciler şu anda kozmik mikrodalga arka alan ışınımındaki desenleri inceliyor. Planck, BICEP ve POLAR BEAR gibi deneyler, üzerine rastgele olmayan bir kuvvetin etkidiğini kanıtlayacak olan polarizasyon araştırması yapıyor. Eğer zamanın etkilerini geri sarar ve bu enerji ile etkileşmiş tüm diğer kuvvetleri aradan çıkarırlarsa, geriye kalan desenin şişme döneminden kalan izler olacağını umuyorlar.
Maldacena ve Arkani-Hamed tarafından öne sürülen desenler daha zor farkedilebilir ve girişime daha duyarlı. O nedenle böyle sinyallerin deneysel olarak bulunmasına daha çok zaman var gibi görünüyor.
Yine de bu araştırma böyle izlerin bulunması ve evrenin tümünde iz bırakmış parçacıklara bakışımızın aydınlanması için bir adım olabilir.
Evrenin sicimlerden oluştuğunu birileri kanıtlasa da kanıtlamasa da, sicim kuramının matematiğinin başka alanlara uygulanabileceği çoktan anlaşıldı.
2009 yılında, araştırmacılar sicim kuramının matematiğinin yoğun madde fiziğindeki geleneksel problemlere uygulanabileceğini keşfetti. O zamandan beri, süperiletkenler üzerine yapılan çalışmalarda sicim kuramından yararlanılıyor.
Kuantum alan kuramına ve süpersimetriye katkılarından ötürü 1990 yılında Field Madalyası alan IAS kuramcısı Edward Witten, bu yılki sicim konferansında gördüğü en yenilikçi çalışmanın Maldacena ile Arkani-Hamed'in araştırması olduğunu belirtti.
Bilimciler LHC'yi bu düzeye kadar çıkaramaz; hatta ona yaklaştıramaz bile. Ama teknolojinin yardımı ve evrenbilimsel çalışmalar aracılığıyla bu parçacıklara ilişkin kanıtları gözlemleme olasılıkları bulunur.
Bilinmeyen Parçacıklar
Şişme (Büyük Patlama'dan 10 ile 33 saniye arasında gerçekleşmiş olan çok kısa süreli aşırı evren büyümesi) sırasında parçacıklar astronomik ölçekte bir güçle çarpışıyorlardı. Bu zamana ait kalıntıları, kozmik arka alan ışınımı adını verdiğimiz kalıntı enerji sisindeki minik çalkantılar olarak görüyoruz. Bilimciler, o sıralarda varolan tarih öncesi parçacıkların kalıntılarını da belki bulabilir.
"Eğer şişme sırasında yeni parçacıklar varolduysa, ilkel çalkalanmalar üzerinde bir iz bırakmış olabilirler. Bunlar belirli desenler şeklinde göze çarpabilir," diyor Princeton İleri Araştırma Enstitüsü'nden kuramcı Juan Maldacena.
Maldacena ve çalışma arkadaşı Nima Arkani-Hamed, bu parçacık desenlerinin neye benzeyebileceği konusunda kuantum alan kuramı hesaplamaları yapmış ve elde ettikleri sonuçları, bu yıl Hindistan'da düzenlenen sicim kuramı konferansında sunmuşlardı.
Minik Sicimler
Sicim kuramı genellikle en temel görüşü ile özetlenir: Maddenin temel birimleri parçacıklar değildir; tek boyutlu, titreşen enerji iplikçikleridir.
Kuramın amacı, kuantum mekaniği ile Einstein'ın genel görelilik kuramı arasındaki matematiksel bir uyuşmazlığı gidermektir. Örneğin bir kara deliğin içinde, kuantum mekaniğine göre kütleçekim imkansızdır. Bir kuramı diğerine uydurmak adına yapılan her türlü girişim, tüm narin sistemin çökmesine yol açar. Bunu denemek yerine, sicim kuramı yepyeni bir matematiksel çatı inşa eder. Bu yapıdan her iki kuram da doğal olarak doğar. Doğanın kuvvetleri zarif bir biçimde birleşir ve bilinen tüm temel parçacıklar doğru niteliklerle tanımlanmış olarak belirir.
Matematiksel bir sistem olarak sicim kuramı muazzam sayıda öngörüde bulunmuştur. Peki bunların ne kadarı test edilebilmiştir? Şimdiye kadar hiçbiri.
Sicimlerin evrendeki en küçük nesneler olduğu düşünülüyor. Parçacık fiziği deneylerindeki ölçekler bile sicimler için devasa büyüklükler anlamına geliyor. Dolayısıyla parçacık fiziği deneyleri üzerinde sicimlerin etkilerini hesaplamak hiç kolay değil. Sicim kuramcıları yeni parçacıkların varlığını öngörebiliyor, ama kütlelerini hesaplayamıyorlar.
Durumu daha da zorlaştıracak biçimde, sicim kuramı birbirlerinden kuvvet, parçacık ve boyut sayılarıyla farklılaşan çeşitli evrenler de tanımlayabiliyor. İncelenebilir enerjilerdeki öngörüler, bu bilinmeyen ayrıntılara bağlı oluyor. Hiçbir deney, gerçekliğin böylesine çoklu alternatifini sunan bir kuramı kanıtlayamaz.
Sicim Kuramını Sınamak
Ama bilimciler sicim kuramını en azından kısmen test edebilecek deneyler yapabilmenin yollarını arıyor. Kuramın öngörülerinden biri, benzersiz bir özelliğe sahip parçacıkların varolduğu yönünde: Spini 2'den büyük olan parçacıklar.
Spin, temel parçacıkların bir özelliğidir. Spinsiz parçacıkların bozunumu simetrik desenler izler. Spinli parçacıkların bozunumu asimetrik olur ve spin arttıkça bu desenler giderek karmaşıklaşır. Böyle parçacıkların çarpışmalarından ortaya çıkan karmaşık bozunum desenleri, evren genişleyip soğurkenki duruma ilişkin izler barındırabilir.
Maldacena ve Arkani-Hamed'e göre, bilimciler spini 2'den büyük olan parçacıkların desenlerini, gökadaların dağılımının ince çeşitlemelerinde veya kozmik arka alan ışınımında bulabilir. Gözlemsel evrenbilimcilerin bu ufak sapmaları görebilmesi için geniş bir uzunluk ölçeği aralığında ilkel çalkalanmaları ölçmesi gerekir.
IAS kuramcıları, eğer böyle büyük kütleli ve yüksek spinli parçacıklar var ise ölçümlerin ne olması gerektiğini hesapladı. Böyle bir parçacığın, fizikçilerin LHC'de bulabileceğinden çok daha büyük kütleli olması gerekiyor.
Zorlu Bir Önerme
Evrenbilimciler şu anda kozmik mikrodalga arka alan ışınımındaki desenleri inceliyor. Planck, BICEP ve POLAR BEAR gibi deneyler, üzerine rastgele olmayan bir kuvvetin etkidiğini kanıtlayacak olan polarizasyon araştırması yapıyor. Eğer zamanın etkilerini geri sarar ve bu enerji ile etkileşmiş tüm diğer kuvvetleri aradan çıkarırlarsa, geriye kalan desenin şişme döneminden kalan izler olacağını umuyorlar.
Maldacena ve Arkani-Hamed tarafından öne sürülen desenler daha zor farkedilebilir ve girişime daha duyarlı. O nedenle böyle sinyallerin deneysel olarak bulunmasına daha çok zaman var gibi görünüyor.
Yine de bu araştırma böyle izlerin bulunması ve evrenin tümünde iz bırakmış parçacıklara bakışımızın aydınlanması için bir adım olabilir.
Sicimlerin Değeri
Evrenin sicimlerden oluştuğunu birileri kanıtlasa da kanıtlamasa da, sicim kuramının matematiğinin başka alanlara uygulanabileceği çoktan anlaşıldı.
2009 yılında, araştırmacılar sicim kuramının matematiğinin yoğun madde fiziğindeki geleneksel problemlere uygulanabileceğini keşfetti. O zamandan beri, süperiletkenler üzerine yapılan çalışmalarda sicim kuramından yararlanılıyor.
Kuantum alan kuramına ve süpersimetriye katkılarından ötürü 1990 yılında Field Madalyası alan IAS kuramcısı Edward Witten, bu yılki sicim konferansında gördüğü en yenilikçi çalışmanın Maldacena ile Arkani-Hamed'in araştırması olduğunu belirtti.
Bu içerik BilimFili.com yazarı tarafından oluşturulmuştur. BilimFili.com`un belirtmiş olduğu "Kullanım İzinleri"ne bağlı kalmak kaydıyla kullanabilirsiniz.
Kaynak ve İleri Okuma
Etiket
Projelerimizde bize destek olmak ister misiniz?
Dilediğiniz miktarda aylık veya tek seferlik bağış yapabilirsiniz.
Destek Ol
Yorum Yap (0)
Bunlar da İlginizi Çekebilir
08 Mart 2016
Evrenin Genişlemesi Simüle Edildi

21 Mart 2017
Evrenin Karanlık Çağını Sona Erdiren Şey Neydi?

09 Temmuz 2015
Evren Bütünüyle Matematiksel Olabilir mi?

12 Ocak 2016
Evrenin Mühendisliğini Yapmamız Mümkün mü?

04 Nisan 2018
Higgs Bozonlarının Gizli Yaşamı