İngiliz matematikçi John Wallis 1655 senesinde, kesirli sayıların sonsuz serilerinin çarpımına dayanan ve pi sayısının hesaplanması için türetilmiş olan formülünü içeren bir kitap yayımladı. Geçtiğimiz haftalarda ise Rochester Üniversitesi'nden araştırmacılar sürpriz bir keşfe imza atarak, bir hidrojen atomunun enerji düzeylerinin kuantum mekaniksel hesaplamaları sırasında aynı formüle ulaştı. Bulgular Journal of Mathematical Physics dergisinde yayımlandı.
"Pi sayısının Wallis formülünün peşinde değildik. Öylece kucağımıza düşüverdi." diyor parçacık fizikçisi Carl Hagen. Kuantum mekaniği dersi öğrencileri için hazırladığı bir problemin çözümünde dikkatini çeken bir trend dolayısıyla matematikçi Tamar Friedmann ile temas kuran Hagen, sonunda bunun pi sayısının Wallis formülünün bir ifadesi olduğunu anlamış.
"Tamamiyle sürpriz oldu. Hidrojen atomu için yazılmış denklemlerin içinden Wallis formülünü elde edince hoplayıp zıplamaya başladım." diyor Friedmann. "Bunun ortaya çıkardığı en önemli şey, fizik ile matematik arasındaki güzel bağ. 17.yüzyıldan kalma bir saf matematiksel formülün, kendisinden 300 yıl sonra keşfedilen fiziksel bir sistemi karakterize ediyor olması nefes kesici."
Kuantum mekaniğinde, varyasyon yaklaşımı denilen teknik kullanılarak, tam çözümleri elde edilemeyen kuantum sistemlerin enerji düzeylerine yaklaştırma yapılabilir. Hagen öğrencilerine bu tekniği öğretirken gerçek yaşamda karşılaşılan bir örnek kullanmak istemiş: Hidrojen atomu. Hidrojen atomu, enerji düzeylerinin tam çözümü yapılabilen nadir kuantum mekaniksel sistemlerden biridir. Bu sisteme varyasyon yaklaşımı uygulayıp, sonucu tam çözüm ile karşılaştırmak suretiyle öğrenciler yaklaştırmadaki hata payını hesaplayabilirler.
Hagen problemi kendisi çözmeye başladığında, bir trend hemen dikkatini çekmiş. Varyasyon hesabının hata payı taban durumu için %15 civarındayken, ilk uyarılmış durum için %10 civarında olup, uyarılmış durumlar büyürken hata payının giderek küçüldüğünü görmüş. Bu alışılmadık birşey, çünkü varyasyon yaklaşımı normalde sadece en düşük enerjilerde iyi yaklaştırmalar yapar.
Hagen bunun üzerine Friedmann'ı arayarak, enerji arttıkça ne olabileceğine bir bakmasını istemiş. Varyasyonal çözümün limitinin, Niels Bohr tarafından 20.yüzyılın başında geliştirilen ve elektron yörüngelerinin tam dairesel alındığı hidrojen modeline yaklaştığını bulmuşlar. Bu tabi Bohr'un "karşılığı bulunma ilkesi" uyarınca beklenen bişeydir. İlke, yarıçapı büyük yörüngeler için kuantum sistemlerin davranışının klasik fizik ile tanımlanabileceğini söyler.
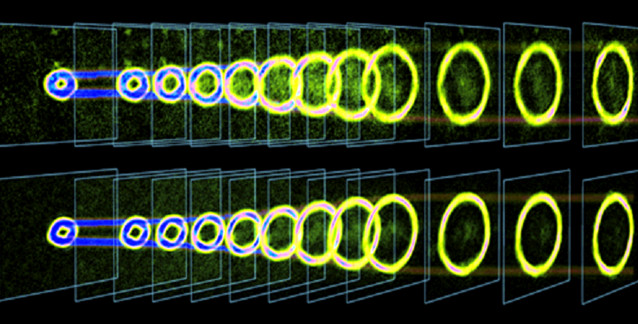
"Düşük enerjili yörüngelerde elektronun izlediği yol dağınık ve bulanıktır. Daha fazla uyarılmış durumlarda, yörüngeler daha keskin tanımlanmış ve yarıçaptaki belirsizlik düşmüş olur." şeklinde açıklıyor Hagen.
- Phys.org, "New derivation of pi links quantum physics and pure math" http://phys.org/news/2015-11-derivation-pi-links-quantum-physics.html
- "Quantum mechanical derivation of the Wallis formula for pi," by Tamar Friedmann and C.R. Hagen, Journal of Mathematical Physics , November 10, 2015. DOI: 10.1063/1.4930800 , http://scitation.aip.org/content/aip/journal/jmp/56/11/10.1063/1.4930800
Dilediğiniz miktarda aylık veya tek seferlik bağış yapabilirsiniz.
Destek OlBunlar da İlginizi Çekebilir