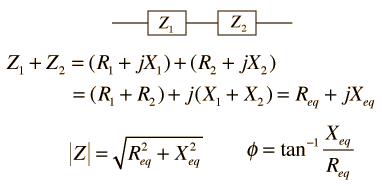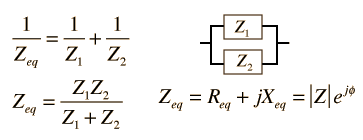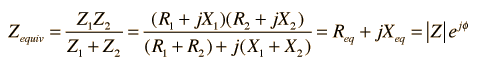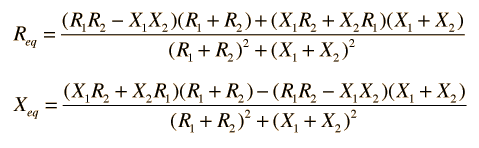Impedance
While Ohm's Law applies directly to resistors in DC or in AC circuits, the form of the current-voltage relationship in AC circuits in general is modified to the form:
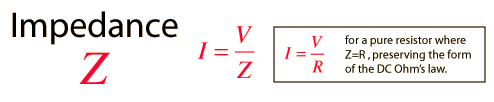
where I and V are the rms or "effective" values. The quantity Z is called impedance. For a pure resistor, Z = R. Because the phase affects the impedance and because the contributions of capacitors and inductors differ in phase from resistive components by 90 degrees, a process like vector addition (phasors) is used to develop expressions for impedance. More general is the complex impedance method.
| Series and parallel combination of any two impedances |
AC circuit concepts
| HyperPhysics***** Electricity and Magnetism | R Nave |