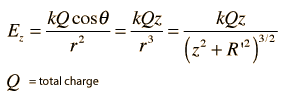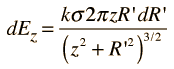Electric Field of Line Charge
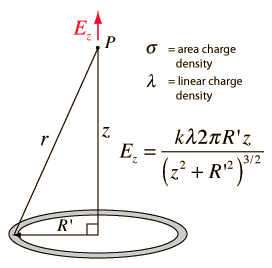
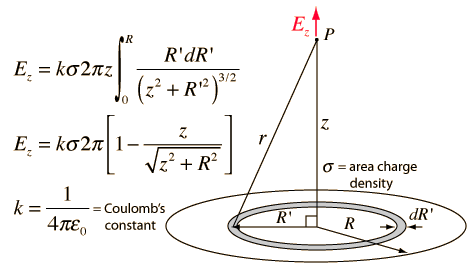
The electric field of a line of charge can be found by superposing the point charge fields of infinitesmal charge elements. The radial part of the field from a charge element is given by
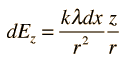
The integral required to obtain the field expression is
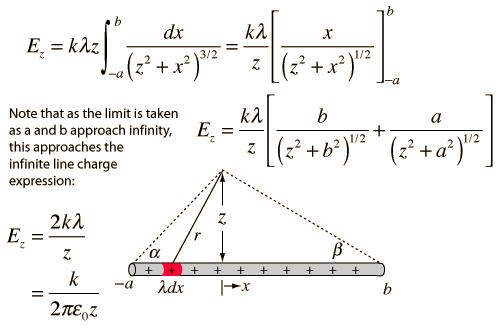
| Infinite line charge |
| Electric potential of finite line charge |
| Fields for other charge geometries |
Electric field concepts
| HyperPhysics***** Electricity and Magnetism | R Nave |