Brezilya'daki bir kelebeğin kanat çırpması Teksas'ta bir kasırgaya sebep olabilir mi? Bu ilginç varsayımsal senaryo, "kelebek etkisi" olarak isimlendirilir ve başlangıç düzeyindeki küçük bir farklılığın gelecekte çok büyük bir sonuca sebebiyet verilmesi olarak tanımlanan kaotik sistemin popüler konseptinin somutlaştırılmış halidir.
Kaosun modellenmesi ve kavranılması birçok bilimsel ve mühendislik sorularının aydınlanmasına yardımcı olabilir, bu yüzden de araştırmacılar kaosa dair daha iyi matematiksel tanımlar geliştirebilmek için çalışıyorlar. Bu tanımlar da, gerçek-dünya kaotik sistemlerine daha benzer modellerin oluşturulmasına yardımcı olabilecek.
University of Maryland'den araştırmacılar; kaosun geçmişte yapılan tanımlarından daha geniş bir perspektife sahip yeni bir tanım geliştirdiler. Pekiştirilmiş bu yeni tanım, sayısal methodlarla kolayca yaklaşılabilir ve çeşitli kaotik sistemlerle geniş ölçüde çalışabiliyor. Keşif; ileride, tıptan meteorolojiye ve daha ötesine kadar farklı disiplinlerden bilgisayar modellemesinin geliştirilmesine yardımcı olabilir.
Chaos 'ta yayımlanan makalenin yazarlarından matematik profesörü Brian Hunt (Institute for Physical Science and Technology- UMD); geliştirdikleri kaos tanımının, bir modelin karanlık köşelerinde pusuda saklanıyor olsa dahi kaotik davranışı tanımladığını söylüyor.
Kaos çalışmaları görece yeni çalışmalar. İlk olarak MIT meteorolojsti Edward Lorenz; 20. Yüzyıl'ın ortalarında hava modellerindeki kaotik karakteristikleri farkederek "kelebek etkisi" kavramını ortaya çıkardı.1963 yılında, Lorenz atmosferik hava akımını tanımlamak için bir dizi diferansiyel denklem yayımladı ve başlangıç koşullarındaki minik varyasyonların zamanla denklemlerin çözümünü dramatik bir biçimde değiştirebildiğini ve uzun vadede hava tahmini yapmanın güçleştiğini belirtti.
Matematiksel olarak, başlangıç koşullarına aşırı hassaslık; Lyapunov üsteli olarak adlandırılan bir nicelikle gösterilebilir. Eğer birbirine son derece yakın olan iki başlangıç noktası; zaman geçtikçe birbirinden katlanarak uzaklaşıyorsa, bu sayı (Lyapunov üsteli) pozitiftir. Lyapunov üstelleri bir kaos tanımı olarak sınırlara sahiptir: yalnızca bir modelin belirli çözümlerindeki kaosu test eder, modelin kendisini değil ve esas model apaçık bir şekilde kaotik kabul edilmek için çok açık olsa dahi bu sınırlar pozitif olabilir.
Uygun bir biçimde, Lorenz denklemlerinin kaotik çözümleri kelebeğin iki kanadı gibi görünür. Şekil; Lyapunov üstelleriyle tanımlanmasının kolay olduğu anlamına gelen matematiksel bir çekici olarak kategorize edilebilir. Ancak Hunt, bütün kaotik davranışların bu kadar açık olmadığını söylüyor.
Örneğin; Hunt, bir pramide sıkıştırılmış dört cam top (yılbaşı ağacı süsleri) tanımlıyor. Işık parlak kürelere çarpıyor ve bütün yönlerde yansıyor. Işığın çoğu basit bir yol boyunca ilerliyor, fakat bazı fotonlar süs topların arasında kaotik şekilde ileri geri sıçrayarak piramidin iç kısmında sıkışık kalabilir. Bu kaotik ışık güzergahları; matematiksel savarlar (kovucu) olarak kategorize edilir ve tam olarak nereye bakacağınızı bilmediğiniz müddetçe kullanılabilecek model denklemleri bulmak zorlaşabilir.
Araştırmacılar; tesisat şebekeleri, asteroid yörüngeleri, kimyasal reaksiyonlar, jeofizik sistemler, kuş sürüleri ve insan organ sistemleri gibi çeşitli doğal ve fiziksel sistemlerde sıklıkla kaotik savarlarla (en. repeller) karşılaşırlar.
Genel olarak kabul görmüş kaos formlarını bir çatı tanımı altına yerleştirmek için, araştırmacılar; entropi olarak adlandırılan bir kavrama yöneldiler. Entropi; zamanla değişen bir sistemde oluşan bozukluk ve belirsizlik oranını ifade eder.
Entropinin kaos için bir proxy (vekalet) olabileceği fikri yeni değil, fakat metrik entropi ve topoloijk entropi gibi entropinin standart tanımları bir "deli gömleğinin" matematiksel eşdeğerlerinde sıkışıp kalıyorlar. Tanımları sayısal olarak uyarlamak zor ve bu tanımlar; bilim insanlarının ilgilendiği birçok biyolojik ve fiziksel sistemlerdeki tanımlara uyarlamayı zorlaştıran ya da imkansız kılan sıkı ön koşullar içeriyor.
Araştırmacıların bu çalışması, entropinin daha gerçekçi modellere uygulanabilen daha esnek bir tipini tanımlıyor; açılım entropisi. Aynı zamanda araştırmacılar; dış faktörlerin, model değiştikçe (evrildikçe) üzerindeki itme ve çekmesini devam ettirdiği sistemleri içererek kaos tanımını genişletiyor. Tanım bir bilgisayar tarafından doğru yaklaşım yapabilir ve potansiyel kaotik girdiler tarafından zorlanan bölgesel hava modelleri gibi sistemlere uyum sağlayabilir.
Araştırmacılar; açılım entropisinin çok geniş bir yelpazedeki model sistemlerindeki kaosları tanımlamada yaygın olarak kullanılan basit bir araç olacağını umut ediyorlar. Bir sistemdeki kaosu nokta atışı olarak saptamak sistemin kontrol edilip edilmeyeceğini belirleyebilmenin ilk adımı olabilir.
Örneğin; Hunt şöyle açıklıyor; farklı başlangıç koşullarına sahip iki aynı kaos sistemi tamamen farklı evrilebilir, fakat eğer sistemler dış girdiler tarafından zorlanırsa, senkronize olmaya başlayabilirler. Kaosun açılım entropisi tanımını uygulayarak ve orijinal sistemin kaotik girdilere cevap verip vermediğini karakterize ederek, araştırmacılar sisteme girişler yoluyla kaos üzerinde biraz kontrol sağlayıp sağlayamayacaklarını açıklayabilirler.
Araştırmacılar; bu tip bir kontrolün; güvenli iletişim sistemlerinin ve daha verimli kalp pillerinin dizayn edilmesinde kullanılabileceğini söylüyorlar.
Araştırma Referansı: Brian R. Hunt and Edward Ott. Defining Chaos. Chaos: An Interdisciplinary Journal of Nonlinear Science, 2015 DOI:10.1063/1.4922973
Kaynak: American Institute of Physics (AIP), "A New Litmus Test for Chaos?", http://www.newswise.com/articles/a-new-litmus-test-for-chaos
Kaosun modellenmesi ve kavranılması birçok bilimsel ve mühendislik sorularının aydınlanmasına yardımcı olabilir, bu yüzden de araştırmacılar kaosa dair daha iyi matematiksel tanımlar geliştirebilmek için çalışıyorlar. Bu tanımlar da, gerçek-dünya kaotik sistemlerine daha benzer modellerin oluşturulmasına yardımcı olabilecek.
University of Maryland'den araştırmacılar; kaosun geçmişte yapılan tanımlarından daha geniş bir perspektife sahip yeni bir tanım geliştirdiler. Pekiştirilmiş bu yeni tanım, sayısal methodlarla kolayca yaklaşılabilir ve çeşitli kaotik sistemlerle geniş ölçüde çalışabiliyor. Keşif; ileride, tıptan meteorolojiye ve daha ötesine kadar farklı disiplinlerden bilgisayar modellemesinin geliştirilmesine yardımcı olabilir.
Chaos 'ta yayımlanan makalenin yazarlarından matematik profesörü Brian Hunt (Institute for Physical Science and Technology- UMD); geliştirdikleri kaos tanımının, bir modelin karanlık köşelerinde pusuda saklanıyor olsa dahi kaotik davranışı tanımladığını söylüyor.
Kaos çalışmaları görece yeni çalışmalar. İlk olarak MIT meteorolojsti Edward Lorenz; 20. Yüzyıl'ın ortalarında hava modellerindeki kaotik karakteristikleri farkederek "kelebek etkisi" kavramını ortaya çıkardı.1963 yılında, Lorenz atmosferik hava akımını tanımlamak için bir dizi diferansiyel denklem yayımladı ve başlangıç koşullarındaki minik varyasyonların zamanla denklemlerin çözümünü dramatik bir biçimde değiştirebildiğini ve uzun vadede hava tahmini yapmanın güçleştiğini belirtti.
Matematiksel olarak, başlangıç koşullarına aşırı hassaslık; Lyapunov üsteli olarak adlandırılan bir nicelikle gösterilebilir. Eğer birbirine son derece yakın olan iki başlangıç noktası; zaman geçtikçe birbirinden katlanarak uzaklaşıyorsa, bu sayı (Lyapunov üsteli) pozitiftir. Lyapunov üstelleri bir kaos tanımı olarak sınırlara sahiptir: yalnızca bir modelin belirli çözümlerindeki kaosu test eder, modelin kendisini değil ve esas model apaçık bir şekilde kaotik kabul edilmek için çok açık olsa dahi bu sınırlar pozitif olabilir.
Uygun bir biçimde, Lorenz denklemlerinin kaotik çözümleri kelebeğin iki kanadı gibi görünür. Şekil; Lyapunov üstelleriyle tanımlanmasının kolay olduğu anlamına gelen matematiksel bir çekici olarak kategorize edilebilir. Ancak Hunt, bütün kaotik davranışların bu kadar açık olmadığını söylüyor.
Örneğin; Hunt, bir pramide sıkıştırılmış dört cam top (yılbaşı ağacı süsleri) tanımlıyor. Işık parlak kürelere çarpıyor ve bütün yönlerde yansıyor. Işığın çoğu basit bir yol boyunca ilerliyor, fakat bazı fotonlar süs topların arasında kaotik şekilde ileri geri sıçrayarak piramidin iç kısmında sıkışık kalabilir. Bu kaotik ışık güzergahları; matematiksel savarlar (kovucu) olarak kategorize edilir ve tam olarak nereye bakacağınızı bilmediğiniz müddetçe kullanılabilecek model denklemleri bulmak zorlaşabilir.
Araştırmacılar; tesisat şebekeleri, asteroid yörüngeleri, kimyasal reaksiyonlar, jeofizik sistemler, kuş sürüleri ve insan organ sistemleri gibi çeşitli doğal ve fiziksel sistemlerde sıklıkla kaotik savarlarla (en. repeller) karşılaşırlar.
Genel olarak kabul görmüş kaos formlarını bir çatı tanımı altına yerleştirmek için, araştırmacılar; entropi olarak adlandırılan bir kavrama yöneldiler. Entropi; zamanla değişen bir sistemde oluşan bozukluk ve belirsizlik oranını ifade eder.
Entropinin kaos için bir proxy (vekalet) olabileceği fikri yeni değil, fakat metrik entropi ve topoloijk entropi gibi entropinin standart tanımları bir "deli gömleğinin" matematiksel eşdeğerlerinde sıkışıp kalıyorlar. Tanımları sayısal olarak uyarlamak zor ve bu tanımlar; bilim insanlarının ilgilendiği birçok biyolojik ve fiziksel sistemlerdeki tanımlara uyarlamayı zorlaştıran ya da imkansız kılan sıkı ön koşullar içeriyor.
Araştırmacıların bu çalışması, entropinin daha gerçekçi modellere uygulanabilen daha esnek bir tipini tanımlıyor; açılım entropisi. Aynı zamanda araştırmacılar; dış faktörlerin, model değiştikçe (evrildikçe) üzerindeki itme ve çekmesini devam ettirdiği sistemleri içererek kaos tanımını genişletiyor. Tanım bir bilgisayar tarafından doğru yaklaşım yapabilir ve potansiyel kaotik girdiler tarafından zorlanan bölgesel hava modelleri gibi sistemlere uyum sağlayabilir.
Araştırmacılar; açılım entropisinin çok geniş bir yelpazedeki model sistemlerindeki kaosları tanımlamada yaygın olarak kullanılan basit bir araç olacağını umut ediyorlar. Bir sistemdeki kaosu nokta atışı olarak saptamak sistemin kontrol edilip edilmeyeceğini belirleyebilmenin ilk adımı olabilir.
Örneğin; Hunt şöyle açıklıyor; farklı başlangıç koşullarına sahip iki aynı kaos sistemi tamamen farklı evrilebilir, fakat eğer sistemler dış girdiler tarafından zorlanırsa, senkronize olmaya başlayabilirler. Kaosun açılım entropisi tanımını uygulayarak ve orijinal sistemin kaotik girdilere cevap verip vermediğini karakterize ederek, araştırmacılar sisteme girişler yoluyla kaos üzerinde biraz kontrol sağlayıp sağlayamayacaklarını açıklayabilirler.
Araştırmacılar; bu tip bir kontrolün; güvenli iletişim sistemlerinin ve daha verimli kalp pillerinin dizayn edilmesinde kullanılabileceğini söylüyorlar.
Araştırma Referansı: Brian R. Hunt and Edward Ott. Defining Chaos. Chaos: An Interdisciplinary Journal of Nonlinear Science, 2015 DOI:10.1063/1.4922973
Kaynak: American Institute of Physics (AIP), "A New Litmus Test for Chaos?", http://www.newswise.com/articles/a-new-litmus-test-for-chaos
Bu içerik BilimFili.com yazarı tarafından oluşturulmuştur. BilimFili.com`un belirtmiş olduğu "Kullanım İzinleri"ne bağlı kalmak kaydıyla kullanabilirsiniz.
Kaynak ve İleri Okuma
Etiket
Projelerimizde bize destek olmak ister misiniz?
Dilediğiniz miktarda aylık veya tek seferlik bağış yapabilirsiniz.
Destek Ol
Yorum Yap (0)
Bunlar da İlginizi Çekebilir
14 Temmuz 2016
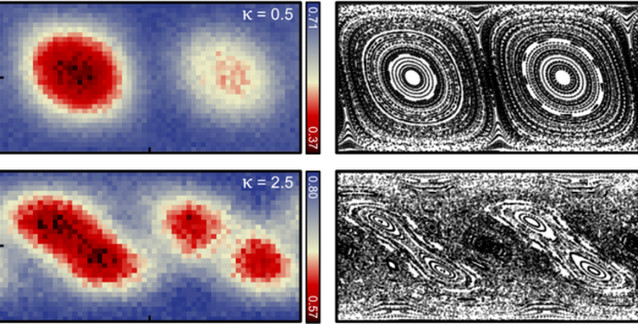
Kaos ve Dolaşıklık Arasında Bağlantı Saptandı

12 Şubat 2019
Evrende Özgür İrade Var mıdır?

04 Kasım 2021
Kaos Teorisi Nedir? Nasıl Keşfedildi?

22 Ocak 2019
Doğa Gerçekten Kaotik ve Fraktal mıdır?