Bu yazımızda, fraktalları keşfeden, tanımlayan ve isimlendiren ünlü matematikçi Benoit Mandelbrot'un çeşitli zamanlarda yaptığı konuşmalardan ve yazılarından seçilen ifadelerinin, soru cümlesi biçimindeki başlıklarla derlenmiş halini sunuyoruz. Dolayısıyla yazı, 2010'da yaşama veda eden Mandelbrot ile yapılmış bir söyleşi gibi görünüyor fakat dediğimiz gibi, farklı zamanlardaki anlatımlarından derlenmiş haliyle...

Çok sayıda karmaşık düşünce ile ilgilenen bir matematikçisiniz. Niçin?

Daireler, elipsler ve paraboller benim gençlik aşkımdı ancak onlara doğada çok nadir rastlanıyor. Galileo bilimde bu şekillerin gerekli olduğunu ileri sürerken kesinlikle haklıydı ancak yeterli olmadıkları ortaya çıktı. Bunun nedeni de dünyanın büyük bölümünün çok pürüzlü ve sonsuz karmaşıklıkta olmasıdır. Kırık bir taş düşünün; herkes onun karmaşık olduğunu söyler. Ben "fraktal" sözcüğünü, Latince'de taş kırıldıktan sonraki durumu ifade eden "fraktus"tan (parçalı) türettim. Bu taş pürüzlü, düzensiz ve parçalanmış durumdadır. Şimdi, kırık bir taşın şeklini nasıl tanımlarsınız? Kırık bir metal parçasının şeklini nasıl tanımlardınız? Çok şaşırtıcı ama pürüzlülüğü tanımlamak için kullanılan prosedürler, son derece yetersiz ve münferit duruma göre olup olayın özünü kavramaktan bütünüyle uzaktı. Oysa ki fraktal geometride sonuç harikulade ve saf bir basitliğe sahip. Öyle şekillerin doğasını tanımlamak için uygun olan dil bu.

Fraktal tam olarak nedir?

Fraktalın tek bir matematiksel tanımı yok. Fraktalın ne olduğunu anlamak için en iyi yol, bir ağaç düşünmektir. Eğer ağacın bir dalına bakarsanız o dalın üzerindeki daha küçük dallarla aslında ağacın bütününe çok benzediğini görürsünüz; ama tabii ağaçtan daha küçüktür. Ondan daha küçük bir dal alırsanız o da yine kendi üzerindeki daha da küçük dallarla ağacın bütününe benzer. Dolayısıyla bir ağaç parçalara ayrılabilir ve her parça ağacın bütününe neredeyse tıpatıp benzer. Son çözümlemede, fraktal yöntemler, kendine benzer (İng. self-similar) parçalardan oluşan doğal ya da yapay her "sistem"i analiz etmek için kullanılabilir.

Öyleyse pürüzlülük ile kendine benzerlik yakından bağlantılı. Peki, ama pürüzlülük gerçekten bu kadar önemli mi?

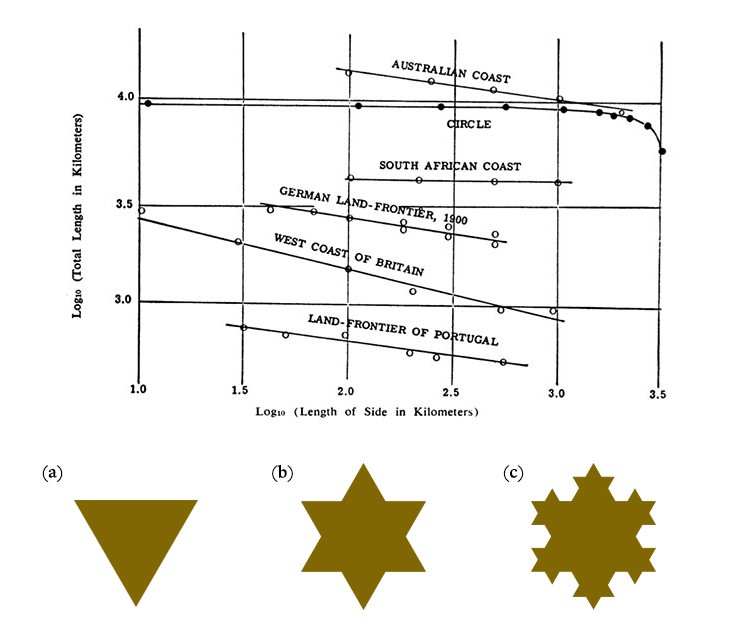
Pürüzlülük doğanın ve kültürün her yanında var. Kıyı şeritlerinin, dağların, bulutların, ağaçların biçiminde; gökadaların dağılımında ve akciğer kanallarında olduğu kadar borda tablolarında, tablolarda, müzikte ya da kimi matematiksel yapılarda karşınıza çıkabilir.

Yani bilimi, günlük hayatta karşımıza çıkan çok sayıda durumla birleştirdiniz.

Kepler'in yaptığını yapabileceğin bir alan tanımlamayı derinden istiyordum; Newton değil, Kopernik değil ama Kepler... Son derece soyut ve herhangi bir uygulamadan uzak bir düşüncenin (bir nevi oyuncağın), bir araca dönüşerek doğanın tüm o karmaşıklığının bir kısmının anlaşılması için kullanılmaya başlanma anını aşırı derecede değerli buluyorum. "Saf" matematiğin gereksinimleri ile Yunan mitolojisindeki kahramanlardan biri olan Antaeus arasında hep bir benzerlik görmüşümdür. Yeryüzü'nün oğlu olan Antaeus'un belirli aralıklarla yere dokunup annesi ile bağını yeniden kurması gerekirdi; aksi takdirde gücünü yitirirdi. Herkül'ün onu alt etmek için yerden yukarı kaldırması yetmişti.

Kendinizi deneysel bir bilimci olarak mı görüyorsunuz?

Kendimi matematiksel bir bilimci olarak görüyorum. Yale Üniversitesi'ndeki makamımın resmi adı bu ve özenle seçilmiş. Çift anlamlı olması da özellikle istenmiş. Farklı bir çağda olsaydık kendime doğa felsefecisi derdim. Kimi insanlar ise bana deneysel felsefeci diyor çünkü bu adlandırmanın kabul edilen başka bir anlamı yok ve benim de özünde bir felsefeci olduğuma kuşku yok. Aynı zamanda fizikçi, iktisatçı ve de bir tür sanatçıyım.

Pek tipik bir akademisyene benzemiyorsunuz.

Hemen her üniversite, nispeten küçük ve oldukça dar kapsamlı olan çeşitli bölümlerin toplu hali olarak tanımlanabilir. Benim çalışmalarım ise bilimin bölümlere ayrılmasının son derece zararlı olduğuna ilişkin güçlü bir inançtan esinleniyor.

O nasıl oluyor?

Bilim, kendini profesyonel sporculuğun bir özelliğine hayret edilecek ve ürkütecek denli indirgemeye istekli olmuştur. Bir atlete yalnızca çok dar kapsamlı bir olay içerisinde değer biçilir. Bana göre, bu durum Olimpiyatları çok sıkıcı bir profesyonel eğlence durumuna sokuyor.

Sizin beğendiğiniz tam tersi.

Benim en hoşuma giden şey, sıradan koşullar altında oldukça farklı ve aralarında organik bir ilişki olmayan olguların, aynı ritimle farklı yönlerde birlikte gelişmiş olan farklı görünüşler olduğu gerçeğidir.

Bu yaklaşımın size ödettiği bir bedel oldu mu?

Bir keresinde, şimdiye göre çok daha gençken, en iyi ABD üniversitelerinden birinden çok çekici bir teklif almıştım ama teklifi ertesi gün geri çektiler. Çünkü dekan benim birkaç başka alanda daha profesyonel etkinlik içinde olmamdan endişelenmiş. Benim var olan bilirkişilik bölümlerinden hangisine girdiğimi bilemediklerinden, üniversite bana iş vermenin bir yolunu bulamadı. İktisat alanında çalışırken de makalelerimde kullandığım yöntemlerin aynı zamanda felsefenin, düzensizliğe ve kaosa ilişkin belirli bir yaklaşımın ve ayrıca fiziğin bir parçası olduğunun bilinmesini çok istiyordum. Her seferinde, dergi hakemleri bunlara ilişkin ifadelerimi çıkarmamı istedi. Daha sonra ben türbülans üzerinde çalışmaya geçtim ve editörler "kuşkulu felsefe" olarak aşağıladıkları kısımları çıkarmam için beni zorladı. Onun yerine daha çok formül ve yöntem ayrıntısı istiyorlardı. Her bir olayda, o alanda bir uzmanmışım gibi davranıyordum.

İktisata ilginiz nasıl başladı?

Temelinde, çok eski bir konu -kişisel gelirin dağılımı yasası- üzerinde önceden yaptığım bazı çalışmalar var. Hendrik S. Houthakker tarafından yönetilen bir Harvard seminerine konuşmacı olarak davet edilmiştim. "Hank'ın" ofisine girmemle beraber, o günü yaşamımın en unutulmaz günlerinden biri yapacak olan sürprizle karşılaştım. Kara tahtada, seminerimde çizmeye niyetlendiğim diyagramın bana tıpatıp aynısı gibi gelen bir diyagram vardı! Hemen sordum, nasıl oluyordu da benim kişisel gelirler hakkında yeni keşfettiğim bir şey halihazırda tahtada duruyordu?  "Neden söz ettiğin hakkında hiçbir fikrim yok. Bu diyagram pamuk fiyatlarını gösteriyor." Meğer ben gelmeden önce bir öğrenci ile çalışıyormuş ve kara tahta henüz temizlenmemiş.

Diyagramlar nasıl o kadar benziyormuş?

Tüm fiyat tabloları birbirine benzer. Tabii bazıları yükselir, bazıları alçalır. Fakat günlük, aylık, yıllık olarak bütüncül görünümlerinde pek de fark olmaz. Tarihleri ve fiyat etiketlerini sildiğinizde hangisinin hangisi olduğunu ayırt edemezsiniz. Eşit derecede kıvrımlıdırlar. Pamuk verilerinde gördüğümüz de işte buydu: Fraktal bir desen. Buradaki fraktal ölçek büyütüp küçültme şekle uygulanmaz. Fraktallık başka türlü bir desende, fiyatların değişme biçimindedir. Finansın özü fraktaldır. O yüzden her şey özüne dönüyor. Houthakker'in pamuk tablosunun benim gelir tabloma benzemesi bir rastlantı değildi. Matematikleri aynıydı.

Apayrı düşünceleri görsel olarak birbirine bağladınız.

Benim bilimsel yaşantımın öyküsü bu: Araştırırken resimlere bakarım, bakarım, bakarım ve onlarla oynarım. Bir resme bir bakış atmak, bilimsel bir aygıttan veri okumak gibidir. Bir kez yapmak asla yeterli olmaz. Büyük bir biyolog ve felsefeci olan Almanya doğumlu bir arkadaşım, bilimdeki ilerlemenin resimleri mümkün olduğunca elemekle ilgili olduğunu ortaya atacak kadar ileri gitmişti. Matematik kusursuzdu çünkü resimlerden bütünüyle kurtuluyordu- en temel ders kitaplarında bile. Ben resimleri geri koydum. Bu durum, meslektaşlarımın çoğu tarafından düşmanca karşılandı. O zamana kıyasla, resimlere olan karşıtlık zayıfladı. Bunun nedeni de olağanüstü verimlilikte olmaları ve insanların sürekli değişmeleri...

Peki, bu çeşit bir aracın kendi tehlikeleri yok mu?

Resimler yol gösterebildikleri gibi insanı aldatabilirler de. Beyin, desen olarak kavradıklarını öne çıkarır; bunu yanlışlayan enformasyonu ise göz ardı eder. İnsan doğası, dünyada düzen ve hiyerarşi görmek için yanıp tutuşur. Bulamadığı yerde de onu icat eder.

Bu düşünce biçimi neden daha yaygın değil?

Bilimde resimlere gereken değer verilmiyor. Onlara güvenilmiyor. Yani kısmen Fransız matematikçiler Lagrange ile Laplace'ın (onlar tüm mantıksal düşünceyi net formüllere ve dikkatle seçilmiş sözcüklere indirgemek için titizlikle çalışmıştı) 200 yıllık mirasından dolayı, dağınık diyagramlar hep kuşkuyla karşılanmıştır. Onların itici gücü, sanıyorum kısmen teknolojikti: O zamanlar çizimler kesinlikten uzak ve masraflıydı; insan elinin ürünüydüler. Fakat bizim yaşadığımız çağda, bilgisayarlar bu durumu tamamen değiştirdi.

Halk arasında, çalışmalarınız sırasında ortaya çıkan güzel fraktal resimlerden bazıları ile ünlüsünüz.

Matematik, güzel şekiller için akıl almaz derecede verimli bir kaynak. Bu şekiller bize sanatçılarla rekabet etme ayrıcalığı tanıyor. Yeni başlayanlar, bu alanda profesyonel değiller ve yarattıkları şekiller büyük ressamların tablolarıyla boy ölçüşemeyebilir. Ama çizmeyi öğreniyoruz. Bilgisayar sanatının Rembrandt veya Picasso'su henüz kendini belli etmedi. Yine de şimdiye dek gördüklerimiz cesaret verici ve belki de formüllü sanat, yeni bir sanat biçiminin başlangıcı olabilir.

Sanat matematiği çekici kılabilir mi?

Arkadaşlarımın çoğu, fraktal geometrinin en harika yanlarından birinin, eşleri ile ilişkilerini iyiye götürmesi olduğunu söyledi. Uzun süredir eşlerine uğraştıkları şeyin olağanüstü güzellikte olduğunu; muhteşem güzellikte bir teoremi, eski bir teoremin inanılmaz güzel bir kanıtını ya da bir şey hakkında harikulade güzellikte bir düşünce biçimini bulduklarını söylüyorlardı. Eşleri de başlarını sallayıp "Tabii canım" diyorlardı. Ama bir gün o eşler ellerinde resimlerle döndüler ve şöyle diyebildiler: "Gördün mü, sana söz ettiğim güzellik böyleydi..."

Fraktal sanatını böylesine özel yapan nedir?

En minimal sanatçının bir çalışmasına bakın ve alıcının birebir kopyasını yapabileceği şekilde bir mektupta o eseri betimlemeyi deneyin. Bunu sözcüklerle yapmak için aşırı derecede uzun bir tanım gerekir. Ama fraktal bir ejderhayı üreten denklem tek satırdan ibarettir. Eğer doğru entelektüel donanıma ve bilgisayar donanımına sahip birine bu denklemi verirseniz onun birebir aynısını üretebilir. Yani bu sanat, tüm sanatların en minimalidir.

Matematik ile sanatın bu şekilde etkileşimi sıradışı bir durum mu?

Matematikçiler, tüm diğer bilimcilerden ve aslında tüm diğer insanlardan farklıdır. Çünkü matematik, insanı hiçbir belirsizliği hoş görmemek üzere eğitir; bu bir gerekliliktir. Ancak biz tartışmalı olduğu kadar eski bir konuyla uğraşıyoruz: Matematiksel kavramların tüm grafik temsilleri bir sanat formudur ve ne kadar basitse o kadar iyidir. Ressam terminolojisiyle konuşmak gerekirse, buna "minimal sanat" denebilir. Bunun birazı M.C. Escher'in mirası mıdır? Öyle olmalı çünkü Escher, Fricke & Klein 1897'de kendisine hiperbolik döşemelerden esinlenme izni verme erdemine sahipti. Fraktal "yeni geometrik sanat", büyük ustaların tablolarına ya da mimarideki güzel sanatlara şaşırtıcı benzerlikler sergiliyor. Fraktal sanat çabucak kabul görebilir çünkü aslında o kadar da yabancı değil.

Eğer sanat ile bağlantı bu denli güçlü ise sanatçıların çalışmanızı dikkate alması gerekir.

Çok sayıda sanatçı, fraktalların doğasını kavrayışlarını ifade edecek bir sözcük dağarcığına sahip değil. Yine de böyle bir anlayış, çalışmalarında kolayca göze çarpıyor.

Birkaç örnek verebilir misiniz?

Fraktal olduğu kesin olan müzik yapan birkaç ekol var. Wuorinen, çalışmalarında güçlü biçimde fraktal temalar kullanıyor ama bu şekilde fraktal müzik bestelemiyor. Gyorgy Ligeti de çok iyi bir arkadaşım. Müzikte hiçbir dilin açıklayamayacağı belli bir yapı olduğuna ilişkin hisleri olduğunu söylemişti. Bunu çocuklara elden geldiğince örnekle anlatmaya çalışmak zorundaydı. Fraktallar hakkındaki kitabı ilk gördüğünde ise söz ettiği yapının fraktal yapıdan başka bir şey olmadığını fark etti ve bu onu çok etkiledi. Benim resimlerimi görene dek müziğin önemli bir yanını anlamamış olduğunu söyledi: Canının istediği gibi yapamazsın çünkü fraktal olması gerekir. Müzik ekolleri, müziğin gürültüden nasıl ayırt edileceğini asla öğretmez. Hem Wuorinen hem de Ligeti, bana gelip en sonunda müziğin neye benzediğini anladıklarını söylemişlerdi. Çünkü onlara genç yaşlarındayken bazı parçaların ayrıntılarının çok az olacağı, bazılarının ise çok ayrıntılı olacağı ve her nasılsa müziğin en başta yapması gereken şeyin küçük, orta ve büyük ayrıntıların uygun bir desenine sahip olması gerektiği öğretilmişti. Eğer Mozart'ın sonaralarından birini dinlerseniz bunu çok iyi görürsünüz: Parçalara bölünmüştür ve sürekli bir şeyler değişir. Bu basit düşünce de müziğin kabul edilebilirliği için en temel gerekliliktir.

Peki ya müziğin dışında?

Rus ressam Wassily Kandinsky, yaklaşık 0,3 m²'lik bir kağıt üzerinde çalışırken kendini filme almıştı. Bütün kağıdı ikiye ayıran bir eğri ile başladı ve daha kısa eğriler eklemeye devam etti. Film durduğunda çok daha kısa eğrilerle çalışmayı sürdürüyordu ve Kandinsky'nin resimlerine baktığımda duyduğum bir hissi doğruluyordu: Fraktallığı anlamıştı. Belki açık bir biçimde değil ama sezgisel olarak anlamıştı. Büyük ölçüde İtalya'da çalışmış olan Fransız ressam Claude Lorrain, gerçekçi olma iddiasında manzaralar çiziyordu. Ama aslında olağanüstü basitleştirilmiş ve fraktal açıdan kolayca yorumlanabilir resimlerdi. Joseph Turner'ın denizde yanan gemileri çizdiği aşırı acayip resimleri de Öklityen ve fraktal şekillere kusursuzca uyar. Eugene Delacroix, "Genç Bir Ressama Öğütler" adlı yazısında fraktallığı içgüdüsel olarak anladığını göstermiştir. Ancak o zamanlarda bunu araştıracak kimse yoktu. Bilimcilerin eksik bıraktığı, ressam ve fotoğrafçıların ise uygulayıp formalize edemediği bir görüngüyü ortaya koyma rolünü yerine getirdiğim için kendimi çok  ayrıcalıklı hissediyorum.

Neden fraktallar özellikle sanatçılar arasında yankı uyandırdı?

M.Ö. 6.yüzyılda  güzellik fikri oldukça kısaydı: Her şeyden önce, güzellik, parça ile bütün arasındaki bir denge anlamına geliyordu. Yetenekli sanatçıların böyle düzenlemeler bulması gerekiyordu; her boydan girdabın bir karışımının dengeli görünüşü gibi... Peki, bunun anlamı, her boydan öğelerin doğal -yani fraktal- bir biçimde dağılımı değil miydi? Kimsenin Paris Opera'nın insana uygun boyutlarda olması gerektiğini söylediğini duymadım; devasa bir bina olmasına rağmen. Neden öyle bir duygu uyandırmaz? Çünkü mimar Charles Garnier, tasarımında her ölçekten ayrıntıları bir araya getirmiştir.

Sanatta yankı bulan başka hangi matematiksel örnekler var?

Öklit'in ilk çevirisi Floransa diline yapılmıştı, yani İtalyanca'ya. Peki, İtalya'da Öklit'i dikkate alan ilk insanlar kimlerdi? Matematikçiler değil, mimarlar ve ressamlardı. Ressamlar, örneğin Giotto, 1300 civarında, perspektifi temsil edecek yollar arıyordu. Başaramadılar. Ta ki sonradan Öklit bilinir ve perspektif sağlam bir duruma gelene dek... 1500 civarında Pierre della Francesca'nın çalışmalarında perspektif öylesine güçlü ve ezicidir ki bunu bir resimde ilk kez gördüğümde uzay ile nesne arasında ayrım var gibi gelmişti. Çoğu insan bu resim etkisinin bilim üzerinde büyük olduğunu düşünüyor. Öyle ki, bilim de sonradan referans noktası ile onlara olan olayları ayırmıştır.

Yani sanat ile bilim arasında çift yönlü bir akış mı var?

Ben, sanatı bilimden ayırmanın ve bu faaliyetleri iletişim halinde olmayan parçalara ayırmanın yanlış olduğunu düşünüyorum. Ölümünden kısa süre önce Feynman'a harika bir ziyaret yapmıştım. Konuştuğumuz tek şey şuydu: Nasıl olur da bir insan, bir şeyin resmini görmeden ve onu elinde tutmadan anladığını iddia edebilir? Kendisi bu şekilde ifade edilemeyen herhangi bir düşüncenin eksik ve kavranamaz olduğu fikrinde ısrarcıydı.

Ya siz? Kendi çalışmanızı sanat olarak görüyor musunuz?

Matematik ile sanatı her gün bir araya getiriyorum. Eğer Alman dili özgürce kunst kullanımına bu kadar gönülsüz olmasaydı bu opera aşığı yaşam çabasını Gesamtkunstwerk olarak betimlerdi.

Fraktal fikri ile güçlü biçimde özdeşleştiniz öyleyse.

Bugün şu söylenebilir: Fraktal geometri organize duruma gelmeden önce, yaşamım fraktal bir yörünge izledi. Ergenliğimden beri beni tetiklemiş olan yaşama ve parlama tutkusunu düşünmeye devam ediyorum. Her kısmi başarı, eski bir beklentiyi ya da açlığı uyandırdı. İronik bir şekilde, aynı şablonla araştırmalarımda da sık sık karşılaşıyorum.

Peki, bu sizi hangi sonuca ulaştırdı?

Matematik, bilim ve güzellik benim zihnimde ayrık faaliyetler değil. Hepsi aynı. Tek bir büyük ve harika alanın farklı köşeleri.